Les rectangles revisités une fois de plus

Apparemment la question sur un pavage de rectangles posée ici il y a quelques jours est stimulante. Après la solution par produit tensoriel, voici une autre qui repose sur une activité habituellement réservée aux enfants: le coloriage. (Les matheux ne sont que de grands enfants !) Merci à David Caisson qui m’a envoyé cette solution extraite du livre Solving Mathematical Problems de Terence Tao.

L’idée de T. Tao est aussi simple que belle: on colore en vert tous les rectangles ayant un côté horizontal entier, et en rouge tous les autres rectangles.
Un argument topologique de connexité nous assure alors que dans le grand rectangle on peut relier les deux côtés verticaux par un chemin vert ou les deux côtés horizontaux par un chemin rouge. (Pour ceux qui ne connaissent pas encore la notion de connéxité : c’est une sorte de théorème des valeurs intermédiaires qui dit que deux lignes reliant les côtés opposés se coupent forcément). Or un chemin vert consiste en la juxtaposition de rectangles verts, donc sa longueur horizontale est entière; et de manière analogue pour un chemin rouge.

Vous pouvez lire la solution complète ici.

Cette « solution » m’a laissé perplexe car sur les trois premières pages l’auteur n’avance pas beaucoup, puis au tout dernier paragraphe il évoque, sans les traiter, quelques obstacles qui pourraient éventuellement se poser. Et avec un peu d’esprit critique on trouve que la démonstration est fausse! Voici un contre-exemple.

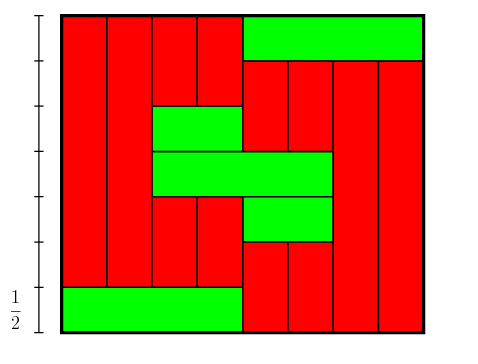
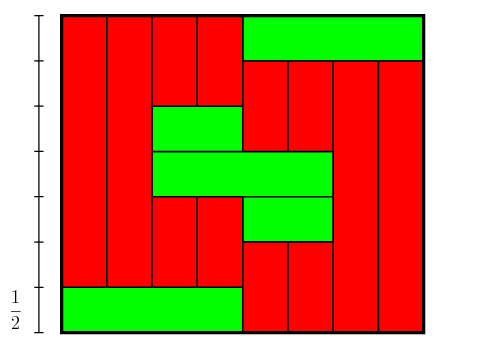
La largeur est 4 et la hauteur est 3,5. Pourtant il n’y a pas de chaîne verte mais seulement une chaîne rouge dont on ne peut rien déduire sur la hauteur (car elle possède des décalages) ni sur la largeur (car les rectangles rouges n’ont pas de largeurs entières).

Mais Terence Tao ne serait pas Terence Tao, porteur de la Médaille Fields 2006 (sorte de prix Nobel pour mathématiciens), si l’idée de sa preuve était entièrement fausse !
En effet, après une petite recherche sur internet, je me rends sur son blog personnel et j’y trouve une liste d’errata où il corrige, entre autres, cette preuve. Voici l’amélioration qu’il apporte:

On colore les rectangles comme avant, mais seulement leurs intérieurs. Ensuite on colore en vert les côtés verticaux ouverts, et le reste en rouge.

Maintenant mon contre-exemple ne résiste plus! On peut relier les deux côtés verticaux par un chemin vert.

Pourquoi cette démonstration améliorée fonctionne-elle ? Et bien, lorsqu’on parcourt un chemin vert disons, alors chaque fois qu’on quitte un rectangle vert pour passer dans un autre, ça se fait sur un segment vertical dont l’abscisse est un entier.

Voilà donc une jolie solution purement topologique, sans analyse. Je ne pense pas qu’elle s’adapte aux dimensions supérieures.