Groupes cycliques (vulgarisation)
Qu’est-ce un groupe cyclique?
Voici une idée pour une activité en mathématiques, accéssible à des élèves en collège. Elle m’est venue en lisant le titre du livre Si 7 = 0 : Quelles mathématiques pour l’école ? de Stella Baruk.
Les heures de la journée — un groupe cyclique d’ordre 24
Calculer dans un groupe cyclique, n’a rien d’abtrait. C’est même une pratique quotidienne de nous tous — littéralement! En effet, pour dire qu’il est minuit certains disent qu’il est 24h et d’autres disent qu’il est 0h. En autres mots, après avoir compté les heures de 0 à 23, donc vingt-quatre fois, on recommence au début en identifiant 24=0. Par conséquence 25=1, 26=2, 27=3, etc.
On dit alors qu’on calcule dans un groupe cyclique d’ordre 24. Il n’y a alors que 24 nombres: 0, 1, 2, … , 23. Il faut bien comprendre que lorsqu’on écrit 25=1 ce n’est pas un égalité entre nombres naturels (elle serait fausse) mais une égalité dans le groupe cyclique d’ordre 24. Le 25 et le 1 sont deux écritures différentes d’un même élément dans ce groupe; et le 49 en est une troisième car 49=24+24+1=1.
Question: Il est 13h. Quelle heure sera-t-il dans 80 heures?
Réponse: On sait que 80h = 3x24h + 8h, donc dans 80 heures il sera 13h+8h=21h.
Nous remarquons dans cet exemple que 8h est le reste de la division de 100h par 24. C’est seulement ce reste qui compte, car les 3x24h correspondent à trois jours et changer de jour ne change pas l’heure.
En général, calculer dans un groupe cyclique d’ordre n revient à identifier n et 0 et par conséquence on identifie également tout nombre avec son reste après division par n.
Voici un autre exemple de notre vie quotidienne. Cette fois pas avec n=24 mais avec n=7.
Les jours de la semaine — un groupe cyclique d’ordre 7
Comptons les sept jours de la semaine: 0 pour lundi, 1 pour mardi, … , 6 pour dimanche. Après le dimanche on retombe sur lundi, c’est-à-dire 7=0. Les jours de la semaine se comptent donc dans un groupe cyclique d’ordre 7. (Dans ce contexte le titre du livre Si 7 = 0 : Quelles mathématiques pour l’école ? de Stella Baruk n’a rien de provocateur!)
Question: Aujourd’hui c’est jeudi le 30/10/2008. Sur quel jour tombe le 30/11/2008? Et le 30/10/2009?
Réponse:
- Entre le 30 octobre et le 30 novembre il y a 31 jours. Or 31=4×7+3, donc le 30/11/2008 tombe trois jours après le jour de départ (jeudi), c’est-à-dire sur un dimanche.
- L’année 2009 n’étant pas bissextile l’expression « dans une année » signifie 365 jours plus tard. Or 365=350+14+1=50×7+2×7+1=52×7+1. Donc le 30/10/2009 sera un jour après le jour de départ (jeudi), c’est-à-dire un vendredi.
Etymologie : d’où vient le nom "groupe cyclique"?
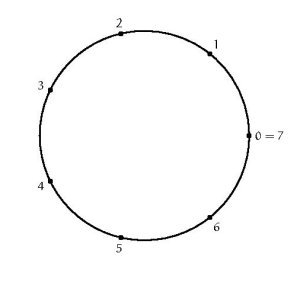
L’illustration en haut par le cercle explique bien le nom: il y a un cycle car, en avançant, on revient sur son point de départ.
C’est donc le contraire de la situation d’une droite où, en avançant, on ne revient jamais sur son point de départ:

Les deux illustrations, les points indiqués sur le cercle ou sur la droite, ont quand-même une chose importante en commun: il existe un élément qui "donne naissance" à tous les autres. C’est ce que les mathématiciens appellent un groupe monogène. Les groupes cycliques sont donc précisément les groupes monogènes finis.
Mais quel est donc cet élément qui donne naissance à tous les autres? Reprenons l’exemple des heures dans la journée, c’est-à-dire du groupe cyclique d’ordre 24. Evidemment l’élément 1 donne naissance à tous les autres car on a 1+1=2, 2+1=3, 3+1=4, … , 23+1=0.
Cet élément générateur est-il unique ? L’élement 2, par exemple, donne-t-il aussi naissance à tous les autres? Evidemment non, car en faisant 2+2=4, 4+2=6, 6+2=8, … , 22+2=0, on ne pourra jamais obtenir un nombre impair.
De la même manière le 3 et le 4 ne donneront pas naissance à tous les autres (testez!). Par contre le 5 fonctionne. En effet, en ajoutant toujours 5 j’obtiens tous les 24 nombres:
5, 10, 15, 20, 25=1, 6, 11, 16, 21, 26=2, 7, 12, 17, 22, 27=3, 8, 13, 18, 23, 28=4, 9, 14, 19, 24=0.
Vous pouvez maintenant refléchir pourquoi ça marche avec le 5 mais pas avec le 2, 3 ou 4. Quelle est la condition pour qu’un élément est générateur du groupe cyclique d’ordre 24?





Coïncidence, j’allais écrire un truc sur l’anneau Z/nZ sur mon blog (enfin il faut que je trouve un peu de temps…).
Une pure question de forme : pourquoi utilisez-vous le format jpeg pour les images, alors que le format PNG est ici bien plus adapté.
Merci, pour la suggestion, je viens de changer les images en format png. Mais je ne vois pas de différence sur mon ecran.
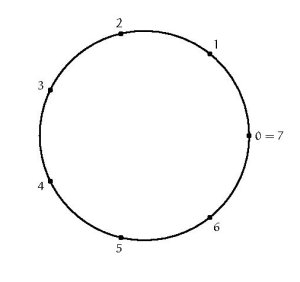
Une remarque pour prolonger un peu : les images représentent respectivement les graphes de Cayley du groupe Z/7Z (pour la partir génératrice {1}) et du groupe Z (pour la partir génératrice {1}).
Plus généralement : à tout couple (G,X) où G est un groupe et X une partie de G, on peut associer un graphe « de Cayley ». Voir fr.wikipedia.org/wiki/Graphe_de_Cayley. Voir en particulier celui d’un groupe libre à deux générateurs : upload.wikimedia.org/wikipedia/commons/d/d2/Cayley_graph_of_F2.svg.
On a un dictionnaire immédiat :
X est génératrice ssi le graphe est connexe.
X est libre (au sens des groupes) ssi le graphe est n’a pas de cycle (c.a.d. est une réunion disjointes d’arbres).
X est une base (au sens des groupes) ssi le graphe est connexe et sans cycle (c.a.d. est un arbre).
Merci pour ces remarques ! Je vais bientôt écrire un peu plus sur certains groupes. Dans ce billet, je voulais rester très très basique — j’y utilise même le mot « groupe » sans que le lecteur doit en connaïtre la signification mathématique…
[à propos de la disparition d’un article]
Que s’est-il passé ? La provocation a été efficace et il y a eu une réaction d’où la suppression de l’article ?
Oui, on pourrait le dire ainsi. Je vous remercie tous pour vos commentaires qui ont donc disparu avec le billet et je reviendrai bientôt à ce sujet (le droit d’auteur)!
simpa ce blog, vos articles et reportages sont trés interressant
Patrick
Histoire de critiquer un peu : si les jours de la semaine forment un groupe cyclique, ça fait quoi lundi + lundi ? 😉 (J’admets, parler d’action de groupe aurait été encore plus pompeux pour un article de vulgarisation !)
(Très bon article au demeurant, je m’en suis un peu inspiré pour ma prochaine note)