Question de probabilités concernant l’étude clinique de Pfizer BionTech
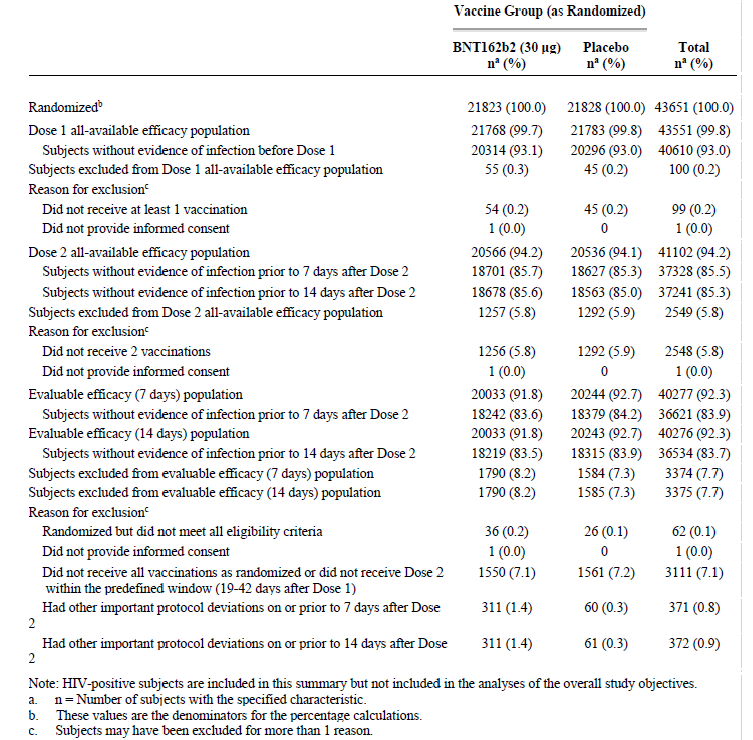
La MHRA (Medicines and Healthcare products Regulatory Agency) de la Grande Bretagne a publié un document intitulé Public Assessment Report, Authorisation for Temporary Supply, COVID-19 mRNA Vaccine BNT162b2 RNA (version mise à jour le 11 juin 2021). Il s’agit d’un rapport expliquant pourquoi le vaccin Pfizer BioNTech a été autorisé. Sur la page 30 on trouve le détail des nombres de participants :
Dans cette étude clinique on choisissait 21823 personnes auxquelles on allait injecter le vaccin et 21828 personnes auxquelles on allait injecter un placebo. Ces deux groupes sont quasiment de même taille ce qui facilite les comparaisons. Il s’agit d’un test en double aveugle, c’est-à-dire que ni la personne injectée ni le surveillant ne savent, durant la durée de l’étude, lequel des deux types d’injection avait lieu.
La dernière ligne de ce tableau donne l’information suivante : À cause de « other important protocol deviations » on a exclu 311 personnes du groupe vaccin, tandis que dans le groupe placebo ce sont seulement 61 personnes. Cela signifie que le nombre de sujets exclus pour des raisons non expliquées en détail est cinq fois plus grand dans le groupe vaccin que dans le groupe placebo.
Dans toutes les 74 pages du rapport je ne trouve aucune explication de cette disparité. Apparemment le MHRA se contente à faire des copier-coller de l’étude du fabriquant au lieu de poser des questions. Est-ce pareil en France ?
Mon devoir d’enseignant est de former des esprits qui réfléchissent à la plausibilité de résultats et qui osent poser de bonnes questions critiques. Donc voici un exercice que j’inclurai dans mon cours de probabilité de cette année.
Exercice : On fait l’hypothèse \(H_0\) l’exclusion pour « other important protocol deviations » est un événement qui a lieu au hasard, de manière indépendante de la personne et de son appartenance au groupe vaccin ou placebo. Si pour chaque personne la probabilité d’exclusion est
\[p={\text{nombre total d’exclus (other important protocol deviations)}\over\text{nombre total de participants}}\]
quelle est la probabilité que parmi les 21823 personnes du groupe vaccin au moins 311 soient exclues?
Voici la réponse: Pour commencer on calcule
\[p={311+61\over21823+21828}\approx0.0085221415.\]Si l’hypothèse \(H_0\) est valide alors on doit calculer \(\mathbb{P}(X\geqslant311)\) lorsque X suit la loi binomiale B(n,p) avec n=21823. Cette loi peut être approchée par la loi normale \(\mathcal N(\mu,\sigma^2)\) avec
\[\begin{align*}
\mu&=np\approx185.9787,\\\sigma^2&=np(1-p)\approx184.3938.
\end{align*}\]On calcule
\[\begin{align*}
\mathbb P(X\!\geqslant\!311)&=\mathbb P\left(X^*\geqslant\frac{311-185.9787}{\sqrt{184.3938}}\right)\\
&\approx\mathbb P(X^*\geqslant9.2)\approx1-\Phi(9.2),
\end{align*}\]où \(\Phi\) désigne la fonction de répartition de la loi normale centrée réduite.
Cette probabilité est quasiment nulle. Bien entendu, sa valeur exacte n’est pas nulle, mais elle est si petite qu’il est dépourvu de sens de vouloir la calculer plus précisément (elle est de l’ordre 10-17).
Voilà donc la réponse à une bonne question. Les responsables du principe de précaution en matière de médicaments ont raté une belle occasion de la poser… et demander des explications.
Mise-à-jour du 10 septembre 2023: Dans cet article deux professeurs allemands calculent la surmortalité en Allemagne durant la campagne de vaccination en 2021 et constatent qu’elle est largement supérieur à celle durant l’année de pandémie 2020, notamment pour la jeune génération. L’un des deux auteurs, professeur de probabilités à l’Université d’Osnabrück, s’explique dans cette vidéo.

Je trouve dans le document
http://www.has-sante.fr/upload/d...
la citation
« Les principales raisons de ces écarts au protocole sont des erreurs de dosage ou d’administration. »
On peut concevoir que ce genre de problème touche plus les non placebo que les placebo. Tout ce qu’on peut conclure est que l’hypothèse faite est fausse (On suppose que l’exclusion pour « other important protocol deviations » est un événement qui a lieu au hasard, de manière indépendante de la personne et son appartenance au groupe vaccin ou placebo)… J’avoue que ça me laisse un peu de marbre étant donné qu’on est de toute façon obligés de croire aux chiffres avancés.
L’article original est apparemment :
http://www.nejm.org/doi/pdf/10.1...
Sauf que les chiffres ne correspondent pas exactement, je ne comprends pas pourquoi c’est le cas (ils reportent 43 548 participants au lieu de 43 651… la différence de 103 ne correspond à rien…). Les chiffres correspondent à peu près, donc soit c’est deux études différentes, soit… j’y comprends rien. Je ne retrouve pas ces chiffres 311, 60 et 61 dans l’article original. Et où sont les références de cet article « Public Assessment Report, Authorisation for Temporary Supply, COVID-19 mRNA Vaccine BNT162b2 RNA » ??? Ça donne pas trop envie de poursuivre.
Merci pour le lien à ces deux articles. Dans celui de la HAS (Haute Autorité de la Santé) on trouve à la page 33 également ces chiffres de 311 et 61 et en effet, contrairement au document britannique, il est indiqué que les principales raisons de ces écarts au protocole seraient des erreurs de dosage ou d’administration.
En revanche je ne conçois pas pourquoi ce genre de problème toucherait plus les non placebo que les placebo lorsqu’il s’agit d’un test en double aveugle.
J’ai peut-être dit ça un peu vite, je ne m’y connais pas. Je voulais dire qu’un « mauvais dosage ou administration » d’un placebo n’est pas très important voire n’a pas de sens, et que ça pouvait expliquer la disparité.
Si 1 personne sur 70 reçoit une injection du vaccin mal dosée c’est beaucoup, et il ne fallait pas l’exclure mais en tenir compte pour des éventuels effets secondaires. Peut-être cela aurait expliqué la surmortalité dans la jeune génération qui avait lieu durant la campagne vaccinale, une surmortalité jamais vue dans les années précédentes.
Un proche de dans ma famille travaille dans une entreprise de biotechnologie. Il y a dix ans il m’a confié, choqué, que leurs études étaient faussées : « Tu sais, dès qu’il y a un problème chez un individu on cherche un prétexte pour l’exclure de l’étude. »