Les rectangles revisités

Par MathOMan, vendredi 28 novembre 2008 à 14:14 - Exo, enigme, casse-tête - Tags - RSS

Dans les commentaires à la question sur un pavage de rectangles notre cher bloggeur PB disait d'avoir entendu de l'existence d'une solution qui utilise le produit tensoriel, mais malheureusement il ne la connaissait pas. D'abord ça m'intrigait — car où est le produit tensoriel dans tout ça? Or finalement un lien entre nos rectangles et cette structure algébrique est assez plausible; en effet, la loi de distributivité des tenseurs

$x\otimes y + x'\otimes y=(x+ x')\otimes y$

devrait correspondre à la fusion de deux rectangles ayant le côté $y$ en commun.

Donc hier j'ai pris le temps d'y réfléchir pour retrouver cette fameuse solution! En fait elle est très simple, sans astuce, elle ne fait qu'utiliser la propriété de distributivité ci-dessus.

Notons $x$ (resp.) $y$ la largeur (resp. hauteur) du grand rectangle $R$ , et de même $x_j$ (resp. $y_j$ ) pour les petits rectangles $R_j, \;j\in J$ , qui partitionnent $R$ . Alors on a

(*) $\sum_{j \in J} x_j\otimes y_j = x\otimes y\,.$

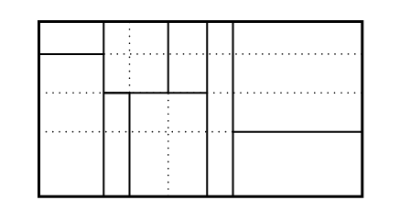
Pour prouver cette égalité il suffit de prolonger les côtés des petits rectangles comme indiqué sur la figure pour avoir une subdivision à laquelle on peut appliquer la propriété de distributivité:

Maintenant on regarde l'égalité (*) dans le produit tensoriel

$\mathbb{R}/\mathbb{Z} \:\otimes_{\mathbb{Z}}\:\mathbb{R}/\mathbb{Z}\,,$

c'est-à-dire on prend les longueurs modulo $\mathbb{Z}$ . D'après hypothèse on a $x_j\otimes y_j = 0$ donc $x\otimes y=0$ et par conséquence $x=0$ ou $y=0$ . En autres mots, la largeur ou hauteur du grand rectangle est entière.

Update : Malheureusement cette preuve est erronée. Cherchez l'erreur... ou lisez mon commentaire no.13 ci-dessous.

Commentaires

1. Le mardi 16 décembre 2008 à 13:33, par Fabien Besnard

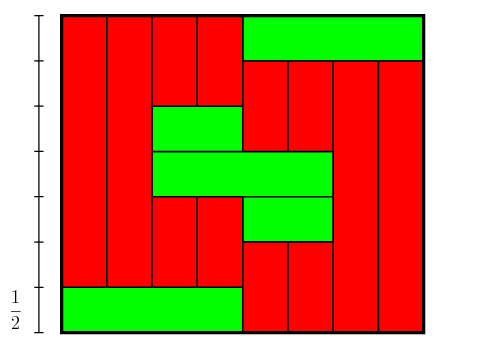
Très belle preuve. Les autres ont l'air plus tordu à côté, mais finalement je crois qu'il y a une même intuition qui sous-tend les trois preuves : l'aire de chaque sous-rectangle est nulle modulo Z, donc l'aire du grand aussi. La façon de donner un sens précis à "aire modulo Z" fait la différence entre la preuve tensorielle (on donne un sens algébrique minimal à cette notion), et la preuve par l'exponentielle qui est plus géométrique, car on intègre la projection de R² sur (R/Z)², ça revient à mesurer une aire mod Z sur le tore. Une idée qu'on peut avoir dès le départ, c'est de tout projeter sur le tore, et de dire que les sous-rectangles se projètent sur des segments géodésiques, d'aire nulle. Le problème est alors de caractériser l'hypothèse que le grand rectangle est l'union des petits en projection sur le tore. Je crois que c'est exactement ce que fait Tao, bien que je n'ai pas lu sa preuve en détail. (J'écris ça un peu rapidemment, j'espère que c'est assez clair.)

2. Le mercredi 17 décembre 2008 à 10:30, par MathOMan

Oui, c'est assez clair pour moi. Le produit tensoriel "force" une multiplication là où elle ne peut pas exister de manière naturelle. Dans notre exemple il n'y a pas de multiplication dans le quotient R/Z car ce n'est pas un anneau, on fait alors un forcing en ecrivant quand même les produits (tensoriels) xy et en exigeant les règles de calcul habituelles pour la multiplication: a(xy)=(ax)y=x(ay) et (x+x')y=xy+x'y et x(y+y')=xy+xy'. L'équation (*) signifie, comme tu le dis, somme des aires = aire totale. Elle a un sens avec des vrais produits dans R, mais si on veut lui donner un sens dans R/Z il faut passer au produit tensoriel.

En revanche, je ne vois pas de lien avec la preuve de Tao ni ce qui peut apporter le fait que (R/Z)² est un tore...

3. Le mercredi 17 décembre 2008 à 16:53, par Fabien Besnard

Tore : ça permet de visualiser le problème, et de comprendre que la preuve analytique n'est pas si mystérieuse que ça ! Le lien avec la preuve de Tao : c'est juste une intuition, et ça fait une heure que j'essaie d'écrire quelque chose pour te l'expliquer, mais je n'y arrive pas. Par contre, ton idée de subdivision m'a donné une autre idée. (Voir commentaire suivant)

4. Le mercredi 17 décembre 2008 à 17:01, par Fabien Besnard

Bon, d'abord, quitte à subdiviser, on peut supposer que les petits rectangles ont soit un côté 1, soit un côté inférieur à 1. Prenons le cas particulier où tous les côtés différents de 1 sont de la forme k/p, où p est un nombre premier (le même pour tous les rectangles). On fait une homothétie de rapport p. Chaque sous-rectangle a maintenant pour côté p et k, donc une aire de kp, donc l'aire du grand est un multiple de p. Maintenant les côtés du grand rectangle sont entiers, car ce sont des réunions disjointes de côtés de sous-rectangles qui sont aussi entiers. Donc p divise le produit des côtés (entiers) du grand rectangle, donc p divise l'un des côtés. En faisant l'homothétie dans l'autre sens, on voit que l'un des côtés du grand rectangle est entier. Maintenant, en utilisant la densité des fractions k/p avec p premier et k<p dans [0;1[, on peut trouver dans le cas général une suite de rectangles partitionnés par des sous-rectangles dont l'un des côtés est de la forme k/p et qui converge vers notre rectangle partitionné initial. Pour tout n, l'un des côtés est entier, on a donc au moins une suite d'entiers qui converge vers la longueur d'un des côtés, elle est donc stationnaire, CQFD. Hmm. ça m'a l'air de marcher.

5. Le jeudi 18 décembre 2008 à 17:57, par Mathoman

Ca va trop vite pour moi! Je ne comprends pas à partir de "Pour tout n..."

6. Le jeudi 18 décembre 2008 à 19:30, par Fabien Besnard

Soit (u_n) une suite de rectangles partitionnés par des sous-rectangles vérifiant la propriété initiale et, de plus, tel que chaque côté non-entier est de la forme k/p_n, pour k entier dépendant du sous-rectangle et p_n un nombre premier n'en dépendant pas, et tel que (u_n) converge vers le rectangle partitionné considéré initialement (appelons-le R). Il est clair qu'une telle suite existe : la seule chose qui bouge ce sont les côtés non-entiers des sous-rectangles, et il y en a un nombre fini et fixé au départ. Pour tout n on peut appliquer le raisonnement précédent et conclure que l'un des côtés du grand rectangle u_n est entier. Or les côtés de u_n tendent vers les côtés de R.

7. Le jeudi 18 décembre 2008 à 19:58, par Fabien Besnard

Tonnerre de Brest ! Je crois bien que l'existence de (u_n) n'est pas si évidente. En faisant bouger légèrement les côtés non-entiers je risque de rendre non-entiers certaints côtés entiers des rectangles adjacents. Il y a (peut-être) une rigidité qui empêche d'utiliser un raisonnement par densité. Pour savoir si ma démo peut être sauvée (ça serait bien car elle est vraiment élémentaire !), il faudrait coder la partition du grand rectangle de façon à voir si on peut bouger un peu les longueurs non-entières ou pas.

8. Le jeudi 18 décembre 2008 à 22:52, par Math O' Man

J'avais donc bien lu et c'était ce point qui ne m'avait pas convaincu. Dès que tu bouges légèrement les rectangles, tu n'as plus de partition exacte, donc tu ne peux pas te ramener au cas initial "k/p partout avec un p fixe".

9. Le jeudi 15 janvier 2009 à 01:58, par PB

Merci pour cette preuve ! C'est tellement naturel. Vive le produit tensoriel ;-)

10. Le jeudi 15 janvier 2009 à 02:05, par PB

Une remarque cependant, à propos de la propriété : si $a\otimes b=0$ alors a=0 ou b=0.

Le produit tensoriel au dessus de Z de Z/2Z et Z/3Z est réduit à 0. En particulier $1\otimes 1=0.$

11. Le vendredi 16 janvier 2009 à 09:44, par MathOMan

Mmmh... c'est surprenant ! J'aurais pensé que $\mathbb{Z}/2\mathbb{Z}\otimes_{\mathbb{Z}} \mathbb{Z}/3\mathbb{Z}=\mathbb{Z}/2\mathbb{Z}$ car

$1\otimes1 + 1\otimes1 = (1+1)\otimes1=0$ donc $1\otimes1 =- 1\otimes1 = 1\otimes(-1)=1\otimes2\:.$

Pour affirmer que $\mathbb{Z}/2\mathbb{Z}\otimes_{\mathbb{Z}} \mathbb{Z}/3\mathbb{Z}=0$ comment montres-tu que $1\otimes1 = 0\:$ ?

12. Le dimanche 18 janvier 2009 à 12:37, par PB

Et bien :

$1\otimes 1=3(1\otimes 1)-2(1\otimes 1)=1\otimes 3-2\otimes 1=1\otimes 0-0\otimes 1=0$

Il nous reste à étudier $(\mathbb{R}/\mathbb{Z})\otimes_{\mathbb{Z}}(\mathbb{R}/\mathbb{Z})$ pour que la preuve sur les rectangles soit complète.

13. Le dimanche 18 janvier 2009 à 22:38, par MathOMan

Olala, là tu m'apprends des choses horribles ! Finalement il y a aussi des diviseurs de zéro dans notre $(\mathbb{R}/\mathbb{Z})\otimes_{\mathbb{Z}}(\mathbb{R}/\mathbb{Z})$ .

$\frac13\otimes \frac12=3\left(\frac13\otimes \frac12\right)-2\left(\frac13\otimes \frac12\right)=1\otimes \frac12-\frac13\otimes 1=0-0=0$
Par conséquence la preuve sur les rectangles ne tient plus )-; Merci à toi, PB, d'avoir eu une lecture critique sur ce point ! Heureusement Tahar Boulmezaoud nous a fourni une autre preuve beaucoup plus élémentaire à laquelle je vais bientôt consacrer un billet sur ce blog.

14. Le mardi 20 janvier 2009 à 10:54, par PB

Ok, j'attend la preuve élémentaire, mais je cherche toujours une preuve avec produit tensoriel :-)

15. Le dimanche 28 juin 2009 à 12:21, par tensor

Une preuve a base de produit tensoriel et de Z-modules, due a T. Coquand, se trouve a l'adresse:

www.cs.chalmers.se/~coqua...

16. Le lundi 29 juin 2009 à 15:34, par wacko

A proof based on tensor product can be found in math intelligencer issue number 4 dec 1997, in the entertainment column. In short, work in the free tensor product $\mathbb{Z}^{(\mathbb{R}/\mathbb{Z})} \otimes \mathbb{Z}^{(\mathbb{R}/\mathbb{Z})}$ .
Use the invariant $c([a,b]\times [c,d]) = (\delta_b-\delta_a) \otimes (\delta_d -\delta_c)$ , where
$\delta_a(x)$ is zero if x is different from a and 1 otherwise. This is an additive function which is zero on semi-integer rectangles only.
Of course you can get ride of tensor product by working with Z-valued functions on
${\mathbb{R}/\mathbb{Z} \times \mathbb{R}/\mathbb{Z}}$ instead.

17. Le samedi 4 juillet 2009 à 11:24, par MathOMan

Voici la version pdf du document de Thierry Coquand (proposé par tensor dans le format ps qu'on ne peut pas lire sur tous les ordinateurs). Il y a une erreur de frappe : sur la page 2 dans l'avant dernière ligne, ça devrait sans doute être $Q_1$ au lieu de $P_1$ .

L'introduction de l'article ne manque pas d'ironie quand il parle de la notion de nombre entier...

18. Le samedi 13 mars 2010 à 09:54, par JLT

En fait, plusieurs preuves sont un cas particulier de celle qui suit :

Etant donné deux applications f:R --> V et g:R --> W vérifiant f(x)=f(y) ssi x-y est entier et g(x)=g(y) ssi x-y est entier, où V et W sont des modules libres sur un anneau intègre K, on définit pour tout rectangle X=[a,b]x[c,d] l'invariant $h(X) = (f(b)-f(a))\otimes_K (g(d)-g(c))\in V\otimes_K W$ . On démontre comme suggéré dans l'article que si X est décomposé en rectangles $X_i$ alors $h(X)=\sum h(X_i)$ . De plus, h(X)=0 si et seulement si X a un côté de longueur entière.

La preuve avec les intégrales correspond à f(x)=g(x)=exp(2 pi i x), V=W=K=C. La preuve du commentaire n°16 correspond à $f(x)=g(x)=\delta_x$ , $V=W={\mathbb{Z}}^{(\mathbb{R}/\mathbb{Z})}, K=\mathbb{Z}$ . C'est en quelque sorte un exemple universel.

Une troisième preuve proche de la preuve fausse de l'article, et plus intuitive que celle du commentaire n°16, consisterait à prendre V=W=K=R, et f(x)=g(x)=x-[x], où [x] désigne la partie entière de x (dans ce cas il n'y a plus besoin de produit tensoriel).

19. Le lundi 15 mars 2010 à 10:41, par MathOMan

Merci pour cette explication. On apprend toujours de ses errreurs !

Ajouter un commentaire

Pourquoi ne pas lire aussi :

Exercice sur un pavage de rectangles

Par Mathoman, vendredi 21 novembre 2008 à 16:02 - Exo, enigme, casse-tête - Tags

Pas si évident que ça!

Appelons un rectangle entier si sa largeur ou sa longueur est un entier.
Soit R un rectangle constitué d'autres rectangles (leur union est R et ils se touchent seulement sur leurs bords).

Questions:

Démontrer que si chacun de ces rectangles est entier, alors le rectangle R l'est aussi.
La réciproque est-elle vraie?
Cet énoncé en dimension deux peut-on le généraliser à des dimensions plus grandes, par exemple aux cubes?

Réponses: Cliquez ici pour la solution. Voir aussi les discussions ici et là.

13 commentaires

Les rectangles revisités une fois de plus

Par Mathoman, dimanche 7 décembre 2008 à 12:16 - Exo, enigme, casse-tête - Tags

Apparemment la question sur un pavage de rectangles posée ici il y a quelques jours est stimulante. Après la solution par produit tensoriel, voici une autre qui repose sur une activité habituellement réservée aux enfants: le coloriage. (Les matheux ne sont que de grands enfants !) Merci à David Caisson qui m'a envoyé cette solution extraite du livre Solving Mathematical Problems de Terence Tao.

L'idée de T. Tao est aussi simple que belle: on colore en vert tous les rectangles ayant un côté horizontal entier, et en rouge tous les autres rectangles. Un argument topologique de connexité nous assure alors que dans le grand rectangle on peut relier les deux côtés verticaux par un chemin vert ou les deux côtés horizontaux par un chemin rouge. (Pour ceux qui ne connaissent pas encore la notion de connéxité : c'est une sorte de théorème des valeurs intermédiaires qui dit que deux lignes reliant les côtés opposés se coupent forcément). Or un chemin vert consiste en la juxtaposition de rectangles verts, donc sa longueur horizontale est entière; et de manière analogue pour un chemin rouge.

Vous pouvez lire la solution complète ici.

Cette "solution" m'a laissé perplexe car sur les trois premières pages l'auteur n'avance pas beaucoup, puis au tout dernier paragraphe il évoque, sans les traiter, quelques obstacles qui pourraient éventuellement se poser. Et avec un peu d'esprit critique on trouve que la démonstration est fausse! Voici un contre-exemple.

contre-exemple à une solution en géométrie

La largeur est 4 et la hauteur est 3,5. Pourtant il n'y a pas de chaîne verte mais seulement une chaîne rouge dont on ne peut rien déduire sur la hauteur (car elle possède des décalages) ni sur la largeur (car les rectangles rouges n'ont pas de largeurs entières).

Mais Terence Tao ne serait pas Terence Tao, porteur de la Médaille Fields 2006 (sorte de prix Nobel pour mathématiciens), si l'idée de sa preuve était entièrement fausse ! En effet, après une petite recherche sur internet, je me rends sur son blog personnel et j'y trouve une liste d'errata où il corrige, entre autres, cette preuve. Voici l'amélioration qu'il apporte:

On colore les rectangles comme avant, mais seulement leurs intérieurs. Ensuite on colore en vert les côtés verticaux ouverts, et le reste en rouge.

Maintenant mon contre-exemple ne résiste plus! On peut relier les deux côtés verticaux par un chemin vert.

dessin d'une exemple pour le problèmes des rectangles entiers

Pourquoi cette démonstration améliorée fonctionne-elle ? Et bien, lorsqu'on parcourt un chemin vert disons, alors chaque fois qu'on quitte un rectangle vert pour passer dans un autre, ça se fait sur un segment vertical dont l'abscisse est un entier.

Voilà donc une jolie solution purement topologique, sans analyse. Je ne pense pas qu'elle s'adapte aux dimensions supérieures.

1 commentaires

Une solution niveau CM2 pour les rectangles entiers

Par Mathoman, samedi 24 janvier 2009 à 20:35 - Exo, enigme, casse-tête - Tags

L'exercice amusant sur les rectangles entiers possède apparemment beaucoup de solutions. François-Xavier Vialard m'a indiqué un article en anglais de Stan Wagon qui réunit les différentes démonstrations de 14 auteurs du monde entier ! L'une parmi elles, qui m'a été signalé aussi par Tahar Boulmezaoud, est particulièrement belle. En effet, elle utilise seulement des mathématiques élémentaires que même un élève de 6^e, voire de CM2, peut comprendre. L'idée de la preuve est de travailler avec un réseau en forme d'échiquier. Voici une description détaillé de cette démonstration, lisible par tous, indépendemment du niveau en maths :

Je rappelle que l'énoncé de l'exercice se trouve ici.

On considère un grand échiquier dont chaque case est de longueur 1/2. Nous allons l'utiliser pour poser nos rectangles dessus.

Lemme 1. Si un rectangle est entier alors il couvre autant de surface noire que blanche.

Preuve : Cela se verra plus facilement avec un dessin. Voici un rectangle dont le coté horizontal est 3.

On le découpe,

puis on déplace la partie gauche à droite, sans que cela ne change la superficie blanche ou noire couverte.

Il est maintenant évident que le rectangle couvre autant de superficie blanche que noire, ce qui achève la démonstration du lemme 1.

Remarque : La réciproque du lemme 1 n'est pas vraie. Comme contre-exemple il suffit de prendre un rectangle dont le milieu se trouve sur un point nœud de l'échiquier. Il couvre alors autant d'aire noire que blanche sans être pourtant nécessairement entier :

Mais si on rajoute une condition de plus les choses s'arrangent ! En effet, on a l'énoncé suivant.

Lemme 1. Si un rectangle dont au moins un sommet coïncide avec un point nœud de l'échiquier couvre autant de surface noire que blanche alors il est entier.

Preuve : Prenons le cas où le sommet en bas à gauche du rectangle coïncide avec un point nœud. Colorons ce nœud ainsi que les autres nœuds qui sont de coordonnées entières par rapport à lui. Nous supposons qu'aucun des autres trois sommets est sur un nœud coloré.

Pour examiner si le rectangle couvre autant de surface blanche que noire, nous le découpons ainsi :

Le rectangle bleu a un côté horizontal entier et couvre donc, d'après le lemme 1, autant de surface noire que blanche. De même pour le rectangle vert car son côté vertical est entier. Il reste alors à examiner le petit rectangle rouge.

Le petit rectangle jaune couvre autant d'aire blanche que noire, tandis que le marron couvre plus d'aire blanche que noire. Par conséquence le petit rectangle rouge couvre plus de surface noire que blanche.

Nous avons donc démontré qu'un rectangle dont un unique sommet coïncide avec un nœud coloré ne peut pas couvrir autant d'aire blanche que noire. Donc si un rectangle a au moins un sommet sur un nœud coloré et couvre la même aire blanche que noire alors il a forcément un deuxième sommet sur un nœud coloré, et cela implique qu'il s'agit d'un rectangle entier. Le lemme 2 est ainsi démontré.

Remarque : En réalité, il y a quatre types petits rectangles restants mais nous n'avons traité qu'un seul type car pour les trois autres on voit immédiatement que les aires blanches et noires ne sont pas les mêmes :

Maintenant nous sommes prêts à donner la preuve du problème posé.

Nous plaçons notre grand rectangle de manière qu'un de ses sommet est sur un point nœud de l'échiquier. Par hypothèse tous les petits rectangles le constituant sont entiers, donc chacun couvre, d'après le lemme 1, autant d'aire blanche et que noire. Il en est de même du grand rectangle. D'après le lemme 2 il est entier.

1 commentaires

Catégories

Les rectangles revisités

Commentaires

Ajouter un commentaire

Pourquoi ne pas lire aussi :

Exercice sur un pavage de rectangles

Les rectangles revisités une fois de plus

Une solution niveau CM2 pour les rectangles entiers

Archives

Blogs de maths

Autres sites

Blogs divers

Syndication