Les rectangles revisités
Dans les commentaires à la question sur un pavage de rectangles notre cher bloggeur PB disait d’avoir entendu de l’existence d’une solution qui utilise le produit tensoriel, mais malheureusement il ne la connaissait pas. D’abord ça m’intrigait — car où est le produit tensoriel dans tout ça? Or finalement un lien entre nos rectangles et cette structure algébrique est assez plausible; en effet, la loi de distributivité des tenseurs
devrait correspondre à la fusion de deux rectangles ayant le côté \(y\) en commun.
Donc hier j’ai pris le temps d’y réfléchir pour retrouver cette fameuse solution! En fait elle est très simple, sans astuce, elle ne fait qu’utiliser la propriété de distributivité ci-dessus.
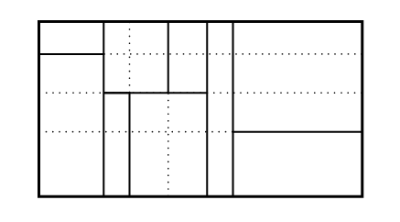
Notons \(x\) (resp.) \(y\) la largeur (resp. hauteur) du grand rectangle \(R\), et de même \(x_j\) (resp. \(y_j\)) pour les petits rectangles \(R_j, \;j\in J\), qui partitionnent \(R\). Alors on a
Pour prouver cette égalité il suffit de prolonger les côtés des petits rectangles comme indiqué sur la figure pour avoir une subdivision à laquelle on peut appliquer la propriété de distributivité:

Maintenant on regarde l’égalité (*) dans le produit tensoriel
\(\mathbb{R}/\mathbb{Z} \:\otimes_{\mathbb{Z}}\:\mathbb{R}/\mathbb{Z}\,,\)
c’est-à-dire on prend les longueurs modulo \(\mathbb{Z}\). D’après hypothèse on a \(x_j\otimes y_j = 0\) donc \(x\otimes y=0\) et par conséquence
\(x=0\) ou \(y=0\). En autres mots, la largeur ou hauteur du grand rectangle est entière.
Update : Malheureusement cette preuve est erronée. Cherchez l’erreur… ou lisez mon commentaire no.13 ci-dessous.


Très belle preuve. Les autres ont l’air plus tordu à côté, mais finalement je crois qu’il y a une même intuition qui sous-tend les trois preuves : l’aire de chaque sous-rectangle est nulle modulo Z, donc l’aire du grand aussi. La façon de donner un sens précis à "aire modulo Z" fait la différence entre la preuve tensorielle (on donne un sens algébrique minimal à cette notion), et la preuve par l’exponentielle qui est plus géométrique, car on intègre la projection de R² sur (R/Z)², ça revient à mesurer une aire mod Z sur le tore. Une idée qu’on peut avoir dès le départ, c’est de tout projeter sur le tore, et de dire que les sous-rectangles se projètent sur des segments géodésiques, d’aire nulle. Le problème est alors de caractériser l’hypothèse que le grand rectangle est l’union des petits en projection sur le tore. Je crois que c’est exactement ce que fait Tao, bien que je n’ai pas lu sa preuve en détail. (J’écris ça un peu rapidemment, j’espère que c’est assez clair.)
Oui, c’est assez clair pour moi. Le produit tensoriel "force" une multiplication là où elle ne peut pas exister de manière naturelle. Dans notre exemple il n’y a pas de multiplication dans le quotient R/Z car ce n’est pas un anneau, on fait alors un forcing en ecrivant quand même les produits (tensoriels) xy et en exigeant les règles de calcul habituelles pour la multiplication: a(xy)=(ax)y=x(ay) et (x+x’)y=xy+x’y et x(y+y’)=xy+xy’. L’équation (*) signifie, comme tu le dis, somme des aires = aire totale. Elle a un sens avec des vrais produits dans R, mais si on veut lui donner un sens dans R/Z il faut passer au produit tensoriel.
En revanche, je ne vois pas de lien avec la preuve de Tao ni ce qui peut apporter le fait que (R/Z)² est un tore…
Tore : ça permet de visualiser le problème, et de comprendre que la preuve analytique n’est pas si mystérieuse que ça ! Le lien avec la preuve de Tao : c’est juste une intuition, et ça fait une heure que j’essaie d’écrire quelque chose pour te l’expliquer, mais je n’y arrive pas. Par contre, ton idée de subdivision m’a donné une autre idée. (Voir commentaire suivant)
Bon, d’abord, quitte à subdiviser, on peut supposer que les petits rectangles ont soit un côté 1, soit un côté inférieur à 1. Prenons le cas particulier où tous les côtés différents de 1 sont de la forme k/p, où p est un nombre premier (le même pour tous les rectangles). On fait une homothétie de rapport p. Chaque sous-rectangle a maintenant pour côté p et k, donc une aire de kp, donc l’aire du grand est un multiple de p. Maintenant les côtés du grand rectangle sont entiers, car ce sont des réunions disjointes de côtés de sous-rectangles qui sont aussi entiers. Donc p divise le produit des côtés (entiers) du grand rectangle, donc p divise l’un des côtés. En faisant l’homothétie dans l’autre sens, on voit que l’un des côtés du grand rectangle est entier. Maintenant, en utilisant la densité des fractions k/p avec p premier et k<p dans [0;1[, on peut trouver dans le cas général une suite de rectangles partitionnés par des sous-rectangles dont l’un des côtés est de la forme k/p et qui converge vers notre rectangle partitionné initial. Pour tout n, l’un des côtés est entier, on a donc au moins une suite d’entiers qui converge vers la longueur d’un des côtés, elle est donc stationnaire, CQFD. Hmm. ça m’a l’air de marcher.
Ca va trop vite pour moi! Je ne comprends pas à partir de "Pour tout n…"
Soit (u_n) une suite de rectangles partitionnés par des sous-rectangles vérifiant la propriété initiale et, de plus, tel que chaque côté non-entier est de la forme k/p_n, pour k entier dépendant du sous-rectangle et p_n un nombre premier n’en dépendant pas, et tel que (u_n) converge vers le rectangle partitionné considéré initialement (appelons-le R). Il est clair qu’une telle suite existe : la seule chose qui bouge ce sont les côtés non-entiers des sous-rectangles, et il y en a un nombre fini et fixé au départ. Pour tout n on peut appliquer le raisonnement précédent et conclure que l’un des côtés du grand rectangle u_n est entier. Or les côtés de u_n tendent vers les côtés de R.
Tonnerre de Brest ! Je crois bien que l’existence de (u_n) n’est pas si évidente. En faisant bouger légèrement les côtés non-entiers je risque de rendre non-entiers certaints côtés entiers des rectangles adjacents. Il y a (peut-être) une rigidité qui empêche d’utiliser un raisonnement par densité. Pour savoir si ma démo peut être sauvée (ça serait bien car elle est vraiment élémentaire !), il faudrait coder la partition du grand rectangle de façon à voir si on peut bouger un peu les longueurs non-entières ou pas.
J’avais donc bien lu et c’était ce point qui ne m’avait pas convaincu. Dès que tu bouges légèrement les rectangles, tu n’as plus de partition exacte, donc tu ne peux pas te ramener au cas initial "k/p partout avec un p fixe".
Merci pour cette preuve ! C’est tellement naturel. Vive le produit tensoriel 😉
Une remarque cependant, à propos de la propriété : si \(a\otimes b=0\) alors a=0 ou b=0.
Le produit tensoriel au dessus de Z de Z/2Z et Z/3Z est réduit à 0. En particulier \(1\otimes 1=0.\)
Mmmh… c’est surprenant ! J’aurais pensé que \(\mathbb{Z}/2\mathbb{Z}\otimes_{\mathbb{Z}} \mathbb{Z}/3\mathbb{Z}=\mathbb{Z}/2\mathbb{Z}\)
car
\(1\otimes1 + 1\otimes1 = (1+1)\otimes1=0\) donc \(1\otimes1 =- 1\otimes1 = 1\otimes(-1)=1\otimes2\:.\)
Pour affirmer que \(\mathbb{Z}/2\mathbb{Z}\otimes_{\mathbb{Z}} \mathbb{Z}/3\mathbb{Z}=0\) comment montres-tu que \(1\otimes1 = 0\:\)?
Et bien :
\(1\otimes 1=3(1\otimes 1)-2(1\otimes 1)=1\otimes 3-2\otimes 1=1\otimes 0-0\otimes 1=0\)
Il nous reste à étudier \((\mathbb{R}/\mathbb{Z})\otimes_{\mathbb{Z}}(\mathbb{R}/\mathbb{Z})\) pour que la preuve sur les rectangles soit complète.
Olala, là tu m’apprends des choses horribles ! Finalement il y a aussi des dans notre \((\mathbb{R}/\mathbb{Z})\otimes_{\mathbb{Z}}(\mathbb{R}/\mathbb{Z})\).
\(\frac13\otimes \frac12=3\left(\frac13\otimes \frac12\right)-2\left(\frac13\otimes \frac12\right)=1\otimes \frac12-\frac13\otimes 1=0-0=0\)
Par conséquence la preuve sur les rectangles ne tient plus )-; Merci à toi, PB, d’avoir eu une lecture critique sur ce point ! Heureusement Tahar Boulmezaoud nous a fourni une autre preuve beaucoup plus élémentaire à laquelle je vais bientôt consacrer un billet sur ce blog.
Ok, j’attend la preuve élémentaire, mais je cherche toujours une preuve avec produit tensoriel 🙂
Une preuve a base de produit tensoriel et de Z-modules, due a T. Coquand, se trouve a l’adresse:
http://www.cs.chalmers.se/~coqua...
A proof based on tensor product can be found in math intelligencer issue number 4 dec 1997, in the entertainment column. In short, work in the free tensor product \(\mathbb{Z}^{(\mathbb{R}/\mathbb{Z})} \otimes \mathbb{Z}^{(\mathbb{R}/\mathbb{Z})} \).
Use the invariant \(c([a,b]\times [c,d]) = (\delta_b-\delta_a) \otimes (\delta_d -\delta_c)\), where
\(\delta_a(x)\) is zero if x is different from a and 1 otherwise. This is an additive function which is zero on semi-integer rectangles only.
Of course you can get ride of tensor product by working with Z-valued functions on
\({\mathbb{R}/\mathbb{Z} \times \mathbb{R}/\mathbb{Z}}\) instead.
Voici la version pdf du document de Thierry Coquand (proposé par tensor dans le format ps qu’on ne peut pas lire sur tous les ordinateurs). Il y a une erreur de frappe : sur la page 2 dans l’avant dernière ligne, ça devrait sans doute être \(Q_1\) au lieu de \(P_1\).
L’introduction de l’article ne manque pas d’ironie quand il parle de la notion de nombre entier…
En fait, plusieurs preuves sont un cas particulier de celle qui suit :
Etant donné deux applications f:R –> V et g:R –> W vérifiant f(x)=f(y) ssi x-y est entier et g(x)=g(y) ssi x-y est entier, où V et W sont des modules libres sur un anneau intègre K, on définit pour tout rectangle X=[a,b]x[c,d] l’invariant \(h(X) = (f(b)-f(a))\otimes_K (g(d)-g(c))\in V\otimes_K W\). On démontre comme suggéré dans l’article que si X est décomposé en rectangles \(X_i\) alors \(h(X)=\sum h(X_i)\). De plus, h(X)=0 si et seulement si X a un côté de longueur entière.
La preuve avec les intégrales correspond à f(x)=g(x)=exp(2 pi i x), V=W=K=C. La preuve du commentaire n°16 correspond à \(f(x)=g(x)=\delta_x\), \(V=W={\mathbb{Z}}^{(\mathbb{R}/\mathbb{Z})}, K=\mathbb{Z}\). C’est en quelque sorte un exemple universel.
Une troisième preuve proche de la preuve fausse de l’article, et plus intuitive que celle du commentaire n°16, consisterait à prendre V=W=K=R, et f(x)=g(x)=x-[x], où [x] désigne la partie entière de x (dans ce cas il n’y a plus besoin de produit tensoriel).
Merci pour cette explication. On apprend toujours de ses errreurs !