Un arbre qui pousse
Dans ce temps de grand froid, je lance un appel au printemps! On fait pousser un arbre selon la règle suivante. De chaque nœud x partent deux branches, l’une vers le nœud x/(1+x) et l’autre vers le nœud (1+x)/x
.
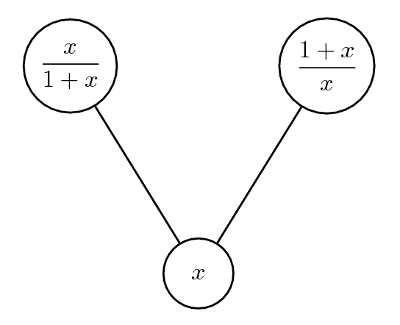 |
On suppose que l’arbre repose sur une racine bien costaud, le nombre 1; et qu’on l’arrose si bien qu’il pousse vers le ciel infiniment haut. Quelle est alors son image, c’est-à-dire l’ensemble des nombres qu’il atteint? Y a-t-il des doublons?

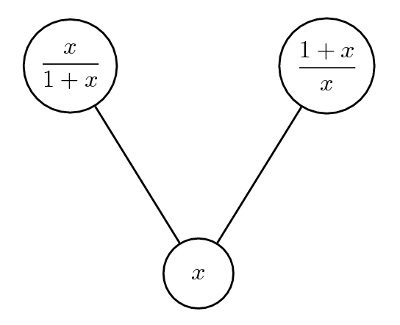


Pas de doublon (par l’absurde).
Je dirais que l’ensemble des nombres atteint est l’ensemble des rationnels strictement positifs, en tout cas il lui est au moins isomorphe, ça doit peut être pouvoir se prouver par récurrence en ordonnant ces nombres avec intelligence…faut que je réfléchisse (dur.)
@Ylrahc : Oui, ce n’est pas si simple. (D’ailleurs je viens d’essayer de laisser un commentaire sur votre blog, mais c’est impossible. Cette restriction est peut-être la raison pourquoi il y a si peu de commentaires sur votre blog?)
J’ai cherché un bon bout de temps, et ce problème est en fait plus facile qu’il n’y paraît: l’arbre contient bien tous les rationnels positifs, et chacun n’apparaît qu’une fois. Je dirais même plus, la profondeur dans l’arbre de chaque rationnel \(\frac{p}{q}\) est égale au nombre d’étapes dans l’algorithme d’Euclide (par soustraction) pour déterminer le PGCD de \(p\) et \(q\).
Pour s’en convaincre, il suffit d’observer tout d’abord que chaque branche gauche sera (strictement) plus petite que 1, et chaque branche droite (strictement) plus grande que 1. Etant donné un rationnel, on peut donc déterminer à coup sûr, s’il est dans l’arbre, d’où il vient. Si \(\frac{p}{q} < 1\), il est la branche gauche de \(\frac{p}{q-p}\), et si \(\frac{p}{q} > 1\), il est la branche droite de \(\frac{q}{p-q}\). N’ayant qu’un ancêtre possible à chaque étape, il ne peut y avoir de doublons.
De plus, en revenant pas à pas à la racine de l’arbre, on effectue bel et bien l’algorithme d’Euclide par soustraction ! Ayant choisi \(p\) et \(q\) premiers entre eux (comme toute représentation d’un rationnel qui se respecte), on arrive bien à 1. Il suffit ensuite de renverser les étapes de l’Algorithme pour arriver au rationnel souhaité à partir de 1.
Bravo, Ylrahc a bien conjecturé et FelixCQ a fourni la preuve. En plus, il a adopté le point de vue élégant qu’il fallait. Et cela malgré l’heure nocturne à laquelle il a posté son commentaire!
Je trouve que c’est une jolie manière de montrer que l’ensemble des nombres rationnels est dénombrable. Ca change de la démonstration habituelle en zig-zag sur les points à coordonnées entières dans le plan.
Héhé, bravo FelixCQ, en réfléchissant un peu aujourd’hui j’avais compris que la clef était la primalité entre eux des numérateurs et dénominateurs (si p et q sont premiers entre eux, ceux des successeurs de p/q [p/(p+q) et (p+q)/p] le sont aussi), prendre le problème à l’envers en trouvant les prédécesseurs et en utilisant l’algorithme d’Euclide est très élégant 🙂
@Mathoman : Merci de l’info, je vais regarder ça. Il est possible que ne puissent poster de commentaires que ceux qui ont un compte authentifié compatible blogger (openID, google). Je vais l’ouvrir aux anonymes. Mais je pense que l’absence de commentaires est surtout due à la très faible popularité du blog 🙂
C’est en effet un très jolie manières de classifier les rationnels ! A-t-elle d’autres implications ?
Si je ne dis pas de bétises, on a à chaque niveau les mêmes rationnels que dans l’arbre de Stern-Brocot, mais dans le désordre !
Pour info: fr.wikipedia.org/wiki/Arb…
Ou encore: mapage.noos.fr/r.ferreol/…