Une génération dyslexique en maths
Je me rappelle qu’une fois, en plein concert à la Philharmonie de Munich, le pianiste Alfred Brendel interrompit son jeu car le public toussait. Il se retournait vers la salle et disait : "Die Grundlage der Musik ist die Stille." Traduction : la base de la musique c’est le silence.
J’aimerais adapter cette phrase aux mathématiques : "La base des mathématiques c’est le calcul". Et je pense au calcul le plus simple, les opérations élémentaires qui devraient être maîtrisées par tous les citoyens d’un pays moderne (à l’exception de quelques rares personnes souffrant d’une sorte de dyslexie des nombres) : addition, soustraction, multiplication et division. Si les élèves ne savent plus calculer, le professeur devrait arrêter son cours, comme Alfred Brendel, et le reprendre plus tard…
Autrefois, grâce à la scolarisation, le savoir progressait d’une génération à l’autre
Dans cet extrait de film des années cinquante un représentant essaie en vain de dissuader Ma and Pa Kettle que 25 divisé par 5 donne 14.
Aujourd’hui c’est le récul: beaucoup de bachéliers ne savent plus calculer
Lorsque j’enseignais en deux classes de terminale ES dans un lycée en région parisienne, j’étais confronté à un problème majeur : le programme du baccalauréat porte sur les dérivées et les intégrales, les logarithmes et les exponentielles. Or la majorité de ces élèves en terminale ne connaissait pas les règles élémentaires de calcul, beaucoup confondaient l’addition avec la multiplication et la soustraction avec la division. Voici un florilège extraits de quelques copies de bacs blancs :
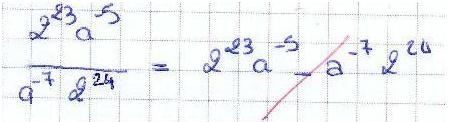
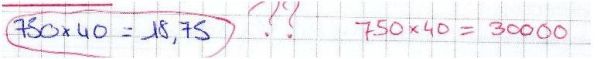
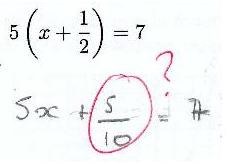
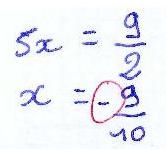
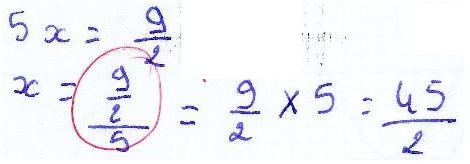
Tout ça pourrait faire rire si ce n’étaient que quelques cas isolés. Mais ce type d’erreurs n’est plus exceptionnel, il est devenu la règle (voir mes statistiques). Il semble qu’aujourd’hui il est impossible de demander à un élève en terminale d’effectuer un calcul élémentaire sans faire d’erreur. Le nombre d’élèves acceptés en première (même en section S) et qui ne connaissent pas la table de multiplication est légion.
Le roi est nu
Certains diront que tout cela n’a pas d’importance car les mathématiques n’interviennent que peu dans notre vie quotidienne et que d’autres facilités sont plus déterminantes pour bien réussir dans la vie. Peut-être. Je serais le dernier à exiger que tous mes co-citoyens connaissent les logarithmes et les intégrales. Mais ce qui me gêne beaucoup c’est que le calcul élémentaire n’est pas acquis et qu’en même temps on habitue les élèves à utiliser un langage de bois mathématique qui prétend qu’il y a une compréhension des objets impliqués tandis qu’au fond rien n’est compris. Sous un splendide manteau de termes savants (intégrales, limites, théorème des valeurs intermédiaires, etc.), le roi est nu ! C’est digne des Impostures intellectuelles à la Sokal-Bricmont…
Evidemment il est impossible, en dernière année de lycée, de rattraper avec des cours de soutien toutes ces bases manquées. Soit on fait les choses correctement dès le départ, soit on ne les fait pas, c’est-à-dire on élimine des programmes scolaires le calcul supérieur avec les fonctions.
Ci-dessous un dernier exemple qui me rend heureux et triste à la fois — triste car cet élève ne maîtrise pas du tout le programme du collège (règles de calcul avec les fractions), et heureux car il a appris ce que je lui enseignais en terminale (règles de dérivation). Mais en fin de compte, quelle est la valeur de ses connaissances en calcul différentiel s’il ne sait pas simplifier correctement la fraction qu’il obtient ?
La question posée était de dériver la fonction \(f(x)=x-\ln(4x-2).\) Voici sa réponse :


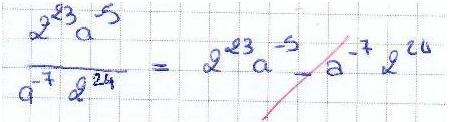



Intéressant mais sans les deux fautes de grammaire et d’orthographe dans le premier paragraphe la forme ne viendrait pas confirmer le fond …
Merci, c’est corrigé maintenant !
Bonjour!
Entre autres lectures intéressantes proposées par votre site, la petite merveille qu’est la vidéo de Ma and Pa… m’a ravie.
Pouvez-vous me communiquer la référence précise du film dont il s’agit?
Bien cordialement
S. B.
C’est Pa and Ma Kettle, une série très populaire aux Etats-Unis des années quarante et cinquante. Au départ c’était une bande desinnée, puis Hollywood l’a adaptée en série de films. Malheureusement je ne peux pas vous dire de quel épisode il s’agit :
Bonjour,
Je découvre ce blog en tant que parent d’un enfant en CM2.
Fichtre ! Moi qui ai abandonné les maths il y a plus de vingt ans, je constate les horreurs documentées.
Par curiosité, j’ai téléchargé le sujet de la série S.
Re-fichtre ! Courbe dessinée, absence d’un bon problème d’algèbre. C’est pourtant loin, mais je me souviens d’un problème portant sur un espace vectoriel de suites réelles dont on sortait, victorieux en quelque sorte, avec fierté.
Actuellement, je ne sais si l’on en retirera un peu de cette joie à la résolution.
Pour se remonter le moral, je vais aller écouter Brendel et les souffleurs germaniques dans les quintettes pour piano et vent de Mozart et Beethoven 😉
Sei mir gegrüsst.
Les profs de maths ne se rendent décidément vraiment pas compte ! La logique mathématique n’est pas donnée à tous; pour des personnes comme moi, c’est avant tout la mémoire qui doit se charger d’enregistrer les règles mathématiques; une fois celles-ci oubliées – et cela arrive forcément un jour, au vu de la quantité d’enseignements accumulée – le raisonnement est extrêmement compliqué à re-réaliser par soi-même.
Alors, la condescendance des profs de maths, franchement ça commence à bien faire; pour miner un élève il y a rien de mieux. Car oui les maths sont une discipline importante, mais c’est dans cette discipline même que s’exprime le mieux l’inégalité des facultés intellectuelles entre personnes.
Oui les maths sont le meilleur moyen de classer les gens, du moins le plus logique, scientifique, mathématique. Mais quel intérêt à un pareil élitisme ? Le mérite n’est pas là, il n’y a que l’orgueil. Donc non, pour moi ça n’est pas par les maths que l’on s’accomplit; et c’est justement l’accomplissement qui compte vraiment, s’ il faut classifier c’est bien à partir de la démarche "existentielle", et certainement pas à partir d’une faculté intellectuelle, bien que son exploitation soit tout à fait respectable. Les chiffres, la logique sont la base de nombreuses choses, galérer en mathématiques n’est pas le signe d’une piètre intelligence, et rendez-vous enfin compte profs de maths que même si pour vous ça en a l’air (et je comprends très bien) ça ne va pas de soi !
Bref, ceci dit heureusement qu’il y a des profs de maths, ça n’est pas que je les méprise, mais si extraterrestres il y a, c’est bien vous, pas par le fait de maitriser les maths bien sûr, mais par le fait d’envisager les rapports humains par les 1 et les 0 ! Damned
Comme toute réaction, la mienne était assez impulsive, et bien qu’un minimum réfléchie, peut-être mal construite et sans trop de recul; je l’espère cependant intelligible.
Bien cordialement,
Timothée
Timothée, si j’ai bien compris, le sujet de ce billet porte sur le calcul…
Le calcul n’est pas seulement une composante des mathématiques, il est aussi nécessaire dans la vie de tous les jours !
Qu’une personne n’arrive pas à dériver, pourquoi pas, elle ne fera pas des études de maths ce n’est pas grave, il faut de tout pour faire des maths.
Par contre qu’une personne ne sache pas calculer, là c’est dangereux… Pour elle et pour les autres ! Et ce n’est pas des maths difficiles !
Si on prend des exemples issus de ce billet, écrire que \(5 \times \dfrac{1}{2} = \dfrac{5}{10} \) ou 750*40 = 18,75, ce n’est pas un problème d’avoir une logique matheuse ou non, c’est un problème de non compréhension du calcul !
Dans la vie de tous les jours, comment cette personne pourra-t-elle acheter des choses si elle ne sait pas calculer ?
Belos tu exagères, il n’y a rien de "dangereux" à ne pas savoir calculer. Avec une bonne calculatrice on s’en sort toujours.
Tu me répondras : "oui mais Timothée risque de se faire avoir dans la vie de tout les jours". Certes tout comme on peut se faire avoir par méconnaissance des lois ou règlements de la vie courante. Tout le monde ne peut pas être juriste et tout le monde ne peux pas être mathématicien.
Timothée, ne prend pas garde aux Aiatolas, il y en a partout. En math bien sûr, mais aussi en français avec les débats sans fin et sans fond sur l’orthographe, en histoire sur l’importance fondamentale de connaitre toute la chronologie des rois de france. En fait, si tu réfléchis bien, il y a des extrémistes dans toutes disciplines. Prend le meilleur de ce qu’ils peuvent te donner et passe ton chemin devant les donneurs de leçons.
@ prof de maths compréhensif : vous dites qu’avec une bonne calculatrice on s’en sort toujours. C’est faux comme montrent mes exemples (voir le premier exercice « calcul de prix »). D’ailleurs vous devriez le savoir et donc je ne peux pas croire que vous êtes vraiment prof de maths.
@ Timothée : vos réactions ne concernent pas le sujet de mon billet. Je ne me moque pas des élèves mais je me plains d’un système qui enseigne des « choses savantes » à des élèves qui, pour divers raisons, ne connaissent plus les fondamentaux et donc ne comprennent en fait rien de ce qu’ils apprennent.
Je ne veux pas que « tout le monde devienne mathématicien », je veux seulement qu’on dise A avant de dire B. Enseigner le calcul des intégrales à des élèves qui ne savent pas calculer l’aire d’un rectangle, c’est du gâchis de temps et d’argent. C’est du brassage d’air qui fait croire aux élèves, aux parents et à la société en général qu’on avance tandis qu’en réalité on recule — ou, pour être plus nuancé (heureusement il existe encore des classes où on apprend toujours correctement) : en donnant le bac à tous ces jeunes l’Éducation Nationale fait croire que la démocratisation de l’enseignement est réussie alors que ce n’est pas vrai.
A mon avis il faut enseigner même moins les mathématiques. Le socle commun doit être acquis par tous, mais le calcul intégral ne doit être appris que par ceux qui sont prêts à l’apprendre..
Je suis tout à fait d’accord avec ce qui est souligné dans ce billet (et heureusement qu’il y a un élève qui a apparemment réussi tous les exercices).
En exemple que le calcul n’est plus maitrisé, mais pire est presque dénigré, il suffit de regarder la nouvelle publicité pour la marque aux deux chevrons :
" Pierre achète une voiture neuve dont le prix est \(\displaystyle{\sqrt{72400}\ \mathrm{euros}-\frac{1}{3}\times 2427}\), bien.
Paul, lui achète un modèle à \(\displaystyle{4539\ \mathrm{euros}\times \pi^2}\), auquel il doit ajouter la TVA à 19,6, d’accord, et soustraire une prime proportionnelle à son âge sachant qu’il a 57 ans. Alors, dire qui de Pierre ou de Paul fait la meilleure affaire. Vous avez quatre heures. "
Bon, au-delà du fait que c’est totalement ahurissant de voir un tel énoncé (à remarquer que Pierre achète une voiture dont le prix est négatif, à savoir qu’on lui donne de l’argent pour qu’il prenne la voiture *rires*), 4 heures pour quelques calculs sans grande difficulté (opérations dans \(\mathbb R\)) c’est vraiment symptomatique du rapport de la société avec le calcul et de ce qui est pointé de ce billet. Petite remarque en plus : le coefficient de proportionnalité n’est même pas précisé, à croire que ceux qui ont écrit cette publicité ont juste pioché des mots mathématiques dans un dictionnaire…
@mathoman : Incroyable cette agressivité! je m’adressait à Belos au sujet de mathématiques de tout les jours, c’est à dire pour l’essentiel des aditions et parfois des multiplications donc parfaitement réalisables par une calculatrice.
D’autre part le propre de la pédagogie c’est la répétition. Le fait d’oublier une règle, même élémetaire, est naturel si on ne l’a pas appliqué depuis longtemps (après 2 à 3 mois de vacances d’été par exemple!) Le cerveau a besoin d’être rafraîchi. Et d’ailleurs, on se rend vite compte qu’une règle déjà apprise est d’autant plus vite retrouvée qu’elle a été travaillée. Or en ce qui concerne les classes ES, on sait que les mathématiques ne sont pas leur point fort. Il faudra donc y passer d’avantage de temps pour la rappeler et ne pas crier des hurlements d’effraie.
Dans la vie de tous les jours, les connaissances de niveau CM2 dans toutes les matières (non seulement les maths, mais aussi le français ou l’histoire-géo) suffisent la plupart du temps. Savoir simplifier une fraction, savoir ce qu’est la révolution française, avoir lu des livres de Victor Hugo sont inutiles dans la vie courante.
Par contre, on utilise des notions plus avancées en maths (ou dans d’autres matières) également dans sa vie professionnelle. Dans cet article, il s’agit d’élèves de terminale ES (Economique et Sociale). On peut supposer que ceux-ci ont besoin de comprendre ce qu’est un taux d’intérêt, un taux d’inflation, un PIB, et même des choses bien plus compliquées. Je ne peux pas croire que ces notions sont vraiment bien comprises si les maths de niveau collège ne sont pas bien assimilées.
A qui la faute? Aux parents, aux élèves, aux professeurs, aux programmes de collège, aux programmes d’école primaire, aux programmes de maternelle, à la société, à la télé, aux iPods, aux téléphones portables, au manque de crédits, au président de la république? Vaste débat, sur lequel je ne tenterai pas de trancher.
@ Vassort et JLT : Merci pour vos interventions.
@ un prof de math compréhensif : Je ne vois pas d’agressivité de ma part, je pensais d’avoir répondu sobrement. N’est-ce pas le cas ?
Si je lis bien votre commentaire du 1er septembre, vous comparez des enseignants comme moi à des « ayatollahs extrémistes » (ça, en revanche, serait plutôt agressif). Je pense que vous et Thimotée, vous n’avez pas compris (ou ne pas lu assez attentivement) le contenu du billet. L’apprentissage des bases du calcul, ce n’est pas une exigence extrémiste ! Vous mettez tout dans le même sac : l’oubli pendant les vacances de certaines règles (comme la dérivation d’un quotient) — c’est excusable — et la non-maîtrise de concepts fondamentaux (comme le calcul d’aire d’un rectangle, la règle des trois, savoir ce que c’est une multiplication) — qui n’est pas excusable. Comme tout concept de base (savoir nager, savoir distinguer entre un verbe et un adjectif), ces notions ne s’oublient jamais, pourvu qu’elles ont été apprises et exigées correctement le moment quand il fallait, c’est-à-dire au collège, bien avant la terminale.
Comme je l’écris dans mon billet je trouve dangereuse cette manie de tout niveler en ne plus faisant de différence entre le « basic stuff and the fancy stuff ».
pour l’essentiel des aditions et parfois des multiplications donc parfaitement réalisables par une calculatrice
J’ai déjà dit en haut que ces calculs de prix et de pourcentage ont été réalisés avec une calculatrice. Si la machine est utilisée par quelqu’un qui n’a pas compris les bases elle ne sert à rien.
Vous trouvez ça bien qu’à la fac on ait recours à ce tableau pour le prix du café ? Et vous pensez que les têtes qui en ont besoin sont capables de comprendre l’intérêt des logarithmes et des exponentielles enseignées en TES ?
Avec une bonne calculatrice on s’en sort toujours.
Une bonne calculatrice… qu’est-ce une mauvaise calculatrice ? 😉
JLT : A qui la faute? … Vaste débat.
Oui.
Vous aussi mathoman je pense que vous n’avez pas compris ou pas lu attentivement ma réponse du premier septembre. Lorsque je parle d’ayatollah je m’adresse à Belos (et pas à vous) qui considère comme dangereux de ne pas savoir faire des opérations élémentaires. Il est dangereux de conduire sans permis, il n’est pas dangereux de ne pas savoir additionner des fractions!
"Vous trouvez ça bien qu’à la fac on ait recours à ce tableau pour le prix du café ?"
Concernant cette phrase, je ne vois vraiment pas le rapport. Je vous rappelle qu’il est bien rare que ce soit les étudiants qui travaillent au CROUS. Bien souvent il s’agit de braves dames très compétentes mais qui n’ont pas fait d’études dépassant le collège. Cet exemple n’est absolument pas représentatif du niveau des étudiant. Cet amalgamme me semble délirant!
Lorsque je parle d’ayatollah je m’adresse à Belos (et pas à vous)
A quoi je pourrais répondre que changer la direction d’un vecteur ne change pas sa longueur 😉 En tout cas, j’aime bien quand ça discute sur mon blog.
Je vous rappelle qu’il est bien rare que ce soit les étudiants qui travaillent au CROUS.
C’est vrai que je n’ai pas pensé que ce tableau pourrait être pour les employées, car il est posé sur la comptoir en direction de la clientèle.
c’est bien de voir un prof de math soucieux que les élèves comprennent (ce n’est pas le cas de tous).
Toutefois, je ne suis pas d’accord quand vous dites que la pédagogie c’est la répétition.
La pédagogie, c’est d’abord se donner les moyens d’évaluer… non pas les élèves mais son enseignement.
Et là, le bas blesse. Le prof de math crois généralement que si l’élève donne le bon résultat à un exercice, c’est que ce dernier à compris, et que donc le cours de math était bon.
Pourtant, il n’a aucun moyen de savoir si l’élève a appliqué un algorithme par coeur, ou s’il a compris ce qu’il manipulait. J’ai été comme vous élève, et j’ai eu des petits camarades, alors j’en sais quelque chose.
Ce qu’un prof de math ne fait jamais, c’est donner des devoirs à rendre sous forme de dissertation (pas d’équation, pas de calcul, pas de graphe) du genre : expliquez moi de ce que vous avez compris de ceci, de cela, qu’est-que représente ça, ou ça. Ce n’est pas anti-mathématiques, les maths se sont faites comme ça durant des centaines (milliers ?) d’années.
Ce genre d’exercices donnerait une chance au prof d’évaluer ce qui a été compris, ce qui ne l’a pas été, repérer les idées fausses, et corriger le tir.
Ce genre d’exercices donneraient aux élèves une chance de plus de conceptualiser, et éventuellement de saisir là où ils bloquent dans leur propre explications.
La répétition peut être utile, mais ce n’est pas de la pédagogie. La pédagogie c’est se donner les moyens de vérifier d’avoir été compris.
Un algorithme s’oublie assez vite. Un concept bien compris se retiens beaucoup mieux, et est plus utile au raisonnement.
Plutôt que de répéter, mieux vaut vérifier ce qui ne passe pas dans la compréhension du concept, et ça les profs de maths ne le font pas ou très rarement, et pas dans le cadre formel d’un devoir à faire. C’est une erreur, c’est dommage, et c’est oublier que c’est ça les maths (et non pas du calcul, comme j’ai pu le lire ici ou là).
A part ça, qu’on ne se méprenne pas, j’apprécie que l’auteur de ce blog se soucie des élèves et de leur compréhension.
Ph.
Ps : pardon s’il y a des fautes, j’ai écrit vite et "en direct" 🙂
Je ne partage pas du tout cet avis très … pédagogie moderne !
NON ! La base de l’apprentissage (pas de la pédagogie ça n’a rien à voir)
c’est bien la répétition ! Je n’ai rien inventé, les grecs le disaient déjà !
Répéter, répéter et encore répéter ad nauseam ! (heureusement pas toujours)
Peut-on imaginer que Brendel cité plus haut ait appris en "méditant" et "comprenant" le contenu profond des oeuvres ?
Je peux affirmer péremptoirement ici PAS DU TOUT ! mais en répétant inlassablement ses morceaux et avant cela des gammes des gammes à en avoir mal partout: à une main, à deux mains, parallèles, mouvement contraire, arpèges de 3ce, 4te, 5te, 6te, 7eme etc etc etc .
La "compréhension" … que de prétention ! Tout à fait dans le style de la pédagogie actuelle. Elle vient éventuellement bien plus tard, lorsqu’à force de répétition on n’y pense même plus ou que l’on a atteint un niveau tel que le problème n’est plus la pratique. D’abord de la pratique.
Les maths ça s’apprend d’abord en pratiquant (comme n’importe quoi) pas en faisant du yoga tout nu dans les montagnes pour "comprendre".
On apprend un langue en répétant son vocabulaire et ses règles de grammaire et pas en méditant sur la construction sémantique et l’histoire de la langue pour "comprendre" pourquoi.
C’est vraiment la dernière des choses dont on doit s’occuper. D’abord un enseignant doit enseigner à savoir faire des choses parce que ça, c’est facile à acquérir par tout élève et ça donne du plaisir "j’ai appris à faire ça"). Puis on monte le niveau doucement et peu à peu se met en place une "certaine compréhension" de ce qui se passe et encore seulement chez certain. Mais au moins par la répétition tout le monde sait "faire". Ceux qui ont "compris" pourront en effet aller plus loin et dans un cadre plus abstrait… plus tard.
A quel âge ais-je "compris" ce que voulait dire \( \forall \epsilon>0, \exist\alpha\)… ? Je pense que j’ai eu l’agreg avant d’avoir "compris". En revanche, je savais "faire".
A mon avis l’on n’a compris que lorsque l’on est capable d’enseigner la chose… autrement dit lorsque l’on maîtrise techniquement le niveau n+2.
Il faudrait demander à un élève de Term d’être capable d’enseigner son propre cours au prétexte qu’il faut qu’il "comprennent".
L’idée des devoirs sans mathématiques où l’on rédige ce que l’on a compris me paraît tout à fait dans la norme d’un pédagogiquement correct qui plaira beaucoup rue de Grenelle. Surtout ne pas demander de calculer quoi que ce soit pour éviter les "excès de technicité". Très à la mode … Si, si ! dans la droite ligne de la suppression de l’intégration par partie en TS. Comme ça, sans changement de variable affine ni Ipp on ne risque aucun "excès de technicité" On reconnaît la dérivée d’une fonction connue ou pas.
Pour en remettre une couche sur la "dys-calculie" actuelle: exemples de mémoire d’une classe de Math-Sup d’un bon lycée:
\( 2x=-\frac12\) alors x=-1
\( (x+1)^2-2x=x^2+2x-2x=x^2\)
\( x^2-3x=0, \Delta=3-0=3\) d’où les racines \( \frac{3\pm\sqrt3}2\)
Des comme ça … 1/4 de la classe à chaque DS.
et je ne parle même pas des innombrables \( P(X^2)=2X^3+X^2\) quand \( P=2X+1\)
Quand on voit ça toutes les semaines… que reste-t-il à faire …
Emigrer en Chine ? en Russie ? Ouvrir un restaurant ?
Mais rue de Grenelle on a déjà la réponse : supprimer du programme la composition des polynômes !
@ rungaldier
D’abord, pour vous exprimer et être entendu, peut-être n’est-il pas nécessaire d’user et abuser des points d’exclamation tout bout de champs, ça donne l’impression que vous criez en permanence sans pour autant donner plus de force à vos arguments.
D’autre part, vous me prêtez (par allusion) des références de pédagogie moderne, des histoires de yoga tout nu dans les montagnes etc : pour un matheux, on s’attendrait à ce que vous sachiez regarder un argument et l’évaluer, voir contre-argumenter sur ce qui est dit, et non pas tenter de noyer le poisson dans des quasi invectives qui n’ont rien de constructif – et vous vous énervez tout seul sans rien connaître de mes positions en matière de pédagogie, et en dévoyant le peu que j’en ai dit.
Votre unique crédo est donc "répéter, répéter, ad nauseum" et surtout "ne pas se poser de questions". C’est le rêve de bien des gens de trouver une réponse simple, unique, à des questions complexes, et d’avoir en face d’eux des gens qui ne posent pas de questions.
Si ça a marché pour vous, très bien. Si vous vous satisfaisez de constater des armées d’élèves qui sortent de l’école relativement dégoutés des maths, je ne pense pas moi pas que ce soit un constat satisfaisant, ni recommandable pour l’avenir des sociétés.
Répéter : c’est très bien pour mémoriser. Je ne suis pas contre. Mais ça ne sers pas à grand chose pour comprendre. Ce ne peut donc pas être une définition de la pédagogie.
D’ailleurs, je ne vois pas la nécessité, si tant est que ce soit possible, de donner une définition de la pédagogie. Cela n’interdit de se poser des question sur la pratique.
La réponse : "répéter, répéter, répéter" me parait simpliste et outrancière.
Vous ne supportez l’idée de demander aux élèves ce qu’ils ont compris, peut-être parce que vous y voyez là une évaluation de votre propre travail. Il est plus facile effectivement de se lamenter sur la nullité des élèves que de se remettre, un tant soit peu, en question. Rien à voir avec le yoga : il y a des bons et des mauvais profs (de yoga aussi, probablement).
L’enseignement des maths tourne en rond depuis des décennies, les progrès n’arrivent pas. A lire l’horreur que vous ressentez à l’idée de la moindre expression littéraire des maths (qui pourtant jalonnent les écrits des plus grands mathématiciens de l’histoire)- la peur que vous ressentez à l’idée de demander aux élèves "ce qu’ils ont compris" – et les manières péremptoires et limite colériques que vous avez de vous exprimer, on se demande vraiment où est passé l’esprit scientifique des lumières.
Je préfère me souvenir de notre chère vieille dame prof de physique au lycée, qui venait avec ses 40 de fièvre nous faire cours pour qu’on ait notre bac, et qui se démenait pour qu’on comprenne ses cours, plutôt que l’attitude de ceux qui méprisent les élèves et surtout surtout surtout : ne veulent voir qu’une tête et pas entendre parler de questions.
Ph.
100% d’accord avec Rungaldier (comme avec ses analyses développées ailleurs).
Malheureusement beaucoup de ceux qui parlent ici n’ont rien connu d’autre qu’un enseignement en ruines, une expérience en maths qui se limite au lycée (version 90-2000), et n’ont donc aucune maîtrise du sujet. L’accumulation de poncifs de la part de Philou est désolante.