Une statistique sur les acquis d’élèves en terminale
En complément de mon billet sur une génération dyslexique en maths voici quelques statistiques. Une analyse avec des idées sur ce qu’on peut encore sauver et sur les conséquences dans l’enseignement supérieur sera donné dans un billet ultérieur. En attendant j’invite mes lecteurs à lire l’article concernant la baisse de niveau sur le blog Mathéphysique.
L’échantillon est constitué des 54 élèves de deux classes de terminale ES d’un même lycée en 2007/2008. Les questions portent sur le calcul élémentaire et ont été posées dans un devoir sur table. L’utilisation de la calculatrice était permise.
Le taux de réussite au bac de ces deux classes était de 55% environ. Si on extrapole avec le taux de réussite au premier exercice ci-dessous, cela signifie qu’au moins 40% des 54 candidats ont obtenu le bac sans savoir interpréter correctement un prix tel qu’il est affiché dans un supermarché.
En publiant ces exemples anonymes, je ne veux pas me moquer des élèves. Nous avons tous fait des erreurs lorsque nous étions élèves, et continuons à en faire — nobody is perfect! Le problème réside dans la fréquence des erreurs (faire des erreurs doit rester l’exception et ne pas devenir la règle) et le type des erreurs (ce ne sont pas de simples erreurs de concentration).
CALCUL D’UN PRIX — 8 élèves ont réussi, taux de réussite: 15%




CALCUL DE POURCENTAGE — 24 élèves ont réussi, taux de réussite: 44%



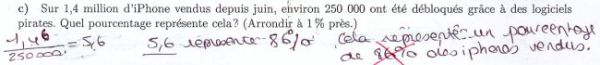
TROUVER UNE EQUATION DE DROITE — 11 élèves ont réussi, taux de réussite: 20%
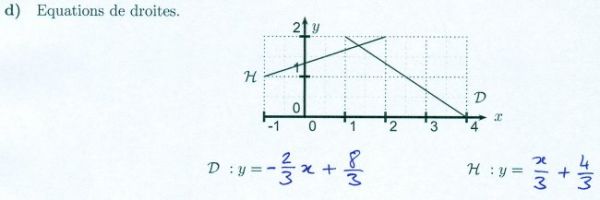
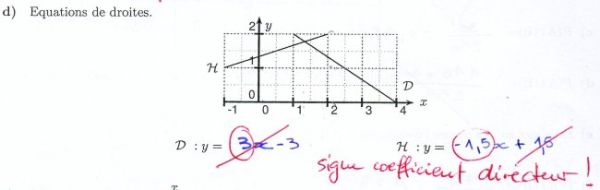
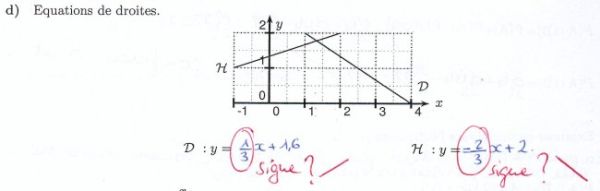
EQUATION DE PREMIER DEGRE — 5 élèves ont réussi, taux de réussite: 9%
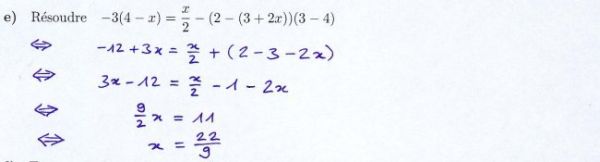
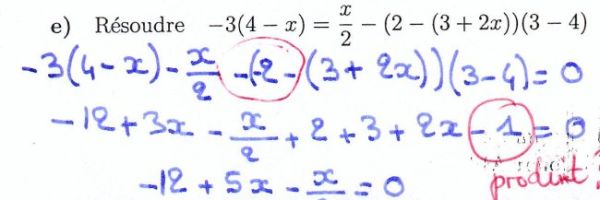
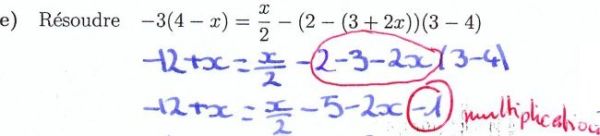
SIMPLIFIER UNE FRACTION — 2 élèves ont réussi, taux de réussite: négligeable
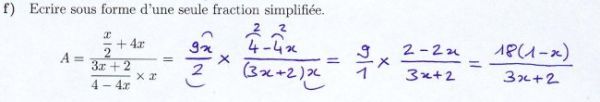

![]()
Autres exemples
- calcul de prix
- calcul de prix
- calcul de prix
- simplification d’une fraction
- simplification d’une fraction
- simplification d’une fraction
- simplification d’une fraction
Remarque:
Les questions étaient regroupées comme premier exercice d’un DST. La barême était indiqué et assurait 1 point par question (sur 20 points dans le devoir complet). Dans « taux de réussite » on a compté les bonnes réponses; l’absence de réponse comptait comme une fausse réponse.



Le constat est assez édifiant.
Les mathématiques me semblent terriblement mal enseignées. Je ne jette pas là la pierre aux enseignants (il y en a des bons et des mauvais, comme partout), mais surtout aux programmes. Les élèves doivent ingurgiter des notions sans avoir les bases pour en comprendre le sens. Ils appliquent donc bêtement des méthodes, mais ne savent pas forcément résoudre des problèmes simples qui ne sont pas exactement ceux fait en cours (et je parle du cours juste avant le contrôle, apprendre bêtement entraîne l’oublie rapide des notions). Bref, on préfère une tête bien pleine à une tête bien faite, et c’est dommage. Cela contribue également au dégoût des mathématique qui sont considérés comme d’obscure opérations sans véritable sens.
P.S. : je vois que vous avez eu Frédéric Pham comme directeur de thèse. Voilà un exemple d’excellent pédagogue!
Visiblement, il y a un problème en calcul élémentaire. Je le constate également avec ma classe : plusieurs de mes élèves écrivent, en début d’année, et malgré un BAC ES tout frais obtenu avec plus de 15 en mathématiques, que (x+2)/2 = x en simplifiant par 2.
Le problème n’est pas vraiment que les élèves écrivent de telles âneries (ça se corrige), mais plutôt qu’on leur donne le BAC avec 15 en math, voire qu’on les fasse passer en terminale, voire qu’on les fasse passer en première, etc.
Ca recoupe également mes observations : beaucoup d’élèves qui ont aujourd’hui le bac n’auraient pas eu leur certificat d’études primaires… parce que justement leurs problèmes viennent de choses qui ne se sont pas fixées au primaire. D’ailleurs PB, quand vous dites que ça se corrige, c’est vrai mais ça se corrige d’autant plus qu’on prend le problème tôt, et en seconde il est déjà bien tard, alors en terminale…
Ceci dit, 55% de réussite au bac ça dénote un niveau très faible, j’imagine que c’est un « lycée difficile » comme on dit pudiquement, ce qui souligne un autre aspect du problème à savoir l’éducation à deux voire trois vitesses.
Enfin, Benoît, je m’excuse de vous le dire brutalement mais vous colportez des idées reçues en parlant de tête bien faite et de tête bien pleine : les extraits de copies que mathoman nous montre ne me semblent pas provenir de têtes bien pleines mais plutôt de têtes bien creuses. C’est à force de slogan de ce type (le sempiternel « apprendre à apprendre »…) que l’on a détruit l’instruction publique et que nous nous trouvons devant cette situation. Si on y réfléchit bien, vouloir faire des « têtes bien faites » est démesurément ambitieux, voire carrément monstrueux (qui juge qu’une tête est bien faite ? qui s’estime lui-même assez intelligent pour apprendre aux autres à l’être ?). Il faut d’abord remplir les crânes avant de commencer à les faire réfléchir, sinon on produit des êtres pour qui la connaissance est accessoire.
Fabien, pourtant ces élèves de terminale qui ne savent pas résoudre ces problèmes très simples en résolvent de bien plus compliqués avec succès en cours. Ces erreurs idiotes montrent bien qu’ils ne savent pas ce qu’ils font et qu’ils n’y comprennent rien. Je ne vois pas où est l’idée reçue. Bien au contraire, on nous fait croire qu’un élève qui bachotte est un bon élève… ce même élève qui oubliera tout ensuite qui a juste appris pour des contrôles mécaniquement sans jamais avoir compris ce qu’ils faisaient. Les têtes sont bien creuses parce qu’au bout d’un moment un savoir sans compréhension s’oublie. Y’a pas de secret.
Apprendre des choses avant de faire comprendre, c’est évident, mais les coupes dans les programmes ont été tellement brutales et stupides qu’ils apprennent un tas de trucs sans jamais faire de rapport entre les différents trucs qu’ils apprennent.
Je n’ai jamais dit qu’il fallait moins leur apprendre. Je pense même le contraire, mais je pense juste qu’il ne suffit pas de leur apprendre un tas de théorèmes pour qu’ils deviennent bons en maths. Il faut d’abord penser à faire un programme cohérent. Je n’ai pas vraiment de solution, et je ne dis pas qu’il est facile de faire un programme de maths. Mais je pense justement qu’il faut cesser d’enlever des choses et en rajouter qui font le lien entre les différents concepts appris.
J’espère bien qu’ils ne vont pas juste se remplir le crâne jusqu’à la terminale, hein. Visiblement, les bases ne sont pas assimilées et on veut leur faire passer le bac (qu’ils auront sans doute en plus).
Ah oui, pour préciser ma pensée, la différence que je fais entre une tête bien pleine et une tête bien faite n’est pas sur le nombre de choses qu’il y aura dedans, entendons-nous bien (apprendre moins pour apprendre mieux, non non non ce n’est pas ce que je veux dire). Plutôt sur le nombre de connexions qu’il existe entre les différents concepts. Je n’entends pas la mesurer dans leur tête, mais dans le programme : il faudrait un programme plus cohérent.
Mais où voyez-vous qu’ils bachotent ?? Quels sont les problèmes si compliqués qu’ils résolvent ? Ils résolvent les problèmes triviaux et répétitifs qu’on a inventé tout exprès pour qu’ils puissent avoir le bac sans rien comprendre à ce qu’ils font. « Il ne suffit pas d’apprendre un tas de théorèmes », mais quels théorèmes ??? Quand j’écris re(z)=(z+\bar z)/2 au tableau je vois la moitié d’un amphi de première année qui fronce les sourcils…
Et de façon très étrange, bon nombre d’entre eux arrivent à comprendre quand même quelque chose dans cette bouillie informe. Pour reprendre votre phrase, les maths ne sont pas mal enseignées : elles ne sont plus enseignées, et l’excellence de la formation mathématique française, reconnue comme l’une des toutes meilleures au monde, a été réduite à néant en une génération…
Cher Fabien, sachez que je suis d’accord avec vous, et que l’opposition qu’il y a a priori entre nous vient surtout du fait que nous ne mettons pas la même chose derrière « avoir une tête bien faite ». J’ai jeté un oeil à votre blog et particulièrement celui auquel vous y faite référence. Eh bien je vous le dis : je suis d’accord avec vous. Ce que j’appelle une tête bien faite n’est pas ce que d’autres en disent… malheureusement.
Les problèmes « compliqués » qu’ils résolvent sont justement des problèmes triviaux si on suit l’algorithme, la méthode. Mais ils ne comprennent pas ce qu’il y a derrière (qui n’est pas si trivial).
Merci pour tous ces commentaires! Evidemment c’est un sujet qui susite le débat.
> pourtant ces élèves de terminale qui ne savent pas résoudre ces problèmes très
> simples en résolvent de bien plus compliqués avec succès en cours.
Non, ce n’est pas le cas. Même s’ils savent, peut-être, que pour trouver le maximum d’une fonction il faut dériver puis résoudre f'(x)=0, ils n’arrivent pas à appliquer ce concept dans le pratique car ils se trompent dès la deuxième ligne de calcul ou ne comprennent pas ce que c’est une équation à une inconnue.
Le but des questions posées ci-dessus était d’isoler ces lacunes du contexte du programme de la terminale. D’abord pour me rassurer, je l’avoue, que le problème ne vient pas de mon cours (je commençais à culpabiliser…), puis pour montrer que les cours de soutien ne devraient pas porter sur le programme de la terminale (intégrales et dérivées) mais sur ce type de calcul élémentaire.
> Ceci dit, 55% de réussite au bac ça dénote un niveau très faible, j’imagine que c’est un “lycée difficile”.
A vrai dire, je ne connais pas le pourcentage pour 2008, mais j’ai cherché celui de années précédentes sur express.fr: 87% en 2005, 78% en 2006 et 57% en 2007. D’après mes impressions en 2008 le taux devrait être proche de celui de 2007.
> Et de façon très étrange, bon nombre d’entre eux arrivent à comprendre quand même
> quelque chose dans cette bouillie informe.
Oui, je crois que ce sont ceux qui n’ont pas vraiment besoin de professeur car ils travaillent de manière assez autonome, par exemple avec un livre. Donc cet enseignement complètement destructuré ne dérange pas trop ces bons élèves, mais détériore les plus faibles qui finalement n’apprennent même plus les bases mathématiques pour se débrouiller dans le vie quotidienne.
> l’excellence de la formation mathématique française, reconnue comme l’une des
> toutes meilleures au monde, a été réduite à néant en une génération…
Je suis entièrement d’accord!
> je vois que vous avez eu Frédéric Pham comme directeur de thèse. Voilà un exemple d’excellent pédagogue!
Oui, je lui dois beaucoup! C’est quelqu’un de très conceptuel qui n’aime pas trop les calculs et essaye de les éviter — par exemple il a écrit un très beau livre où on intègre sur des variétés sans parler de partition d’unité…
Bon, alors il s’agit d’un malentendu entre Benoît et moi. C’est que, j’ai tellement entendu le « tête bien faite vs tête bien pleine » pour justifier des coupes sombres dans les programmes qu’à la moindre occurence, je sors mon revolver…
Mathoman : je ne suis pas aussi optimiste concernant les bons élèves : ils pâtissent du système comme les autres, en particulier ceux des milieux les moins favorisés. Je me souviens encore d’une petite élève de 5e dans un collège de ZEP, qui avait un an de moins que ses camarades mais était à 100 coudées au dessus d’eux. Elle finissait tous les exercices que donnait la prof en 10 minutes quand il fallait une demi-heure aux autres. Pour la récompenser, la prof lui donnait à faire… un dessin ! J’étais simple observateur à l’époque, mais je m’en veux de ne pas avoir réagi et de ne pas être allé moi-même lui donner un exercice plus difficile.
Pour Fabien Besnard : il n’y a pas de souci, même si j’avoue que j’ai été un peu vexé au début, je comprends tout à fait votre agacement.
Pour Mathoman : maintenant que vous avez identifié les difficultés, que pensez-vous qu’il faille faire ? Je ne parle pas des changement à faire dans le système, mais ce sur quoi vous pouvez agir en tant qu’enseignant. J’imagine que leur faire refaire des bases de calcul est difficilement envisageable (à part en cours de soutient, comme vous le soulignez), surtout qu’il y a un programme a boucler dans un temps qui est fini. Bien entendu, les autres commentateur de ce billet qui semblent egalement enseigants ont peut-être des réponses (ou des pistes).
En terminale, il faut être honnête on ne peut plus faire grand chose sur de l’algèbre élémentaire. Il faut bien sûr corriger toutes les erreurs en espérant qu’il y en ait un ou deux à qui ça profite, mais guère plus. Et il faut donner beaucoup de travail à la maison, et corriger tout ça… On peut agir un peu plus en seconde. La première chose à faire est de neutraliser les cons : ceux qui ne veulent rien faire et ne savent pas pourquoi ils sont là. Il n’y en a guère plus de 2 ou 3 par classe, mais si on les laisse faire il peuvent empêcher tous les autres de travailler. Déjà ça, ça prend du temps et pas mal d’énergie, mais une fois qu’on a gagné on peut bosser sérieusement. On peut utiliser l’heure d’aide individualisée pour faire systématiquement de l’algèbre, et avec toute la classe ou presque. C’est interdit, mais il faut le faire quand même… (ça implique de se battre avec la direction qui en général colle des cours d’option pendant vos AI et qui fait que vous ne pouvez pas convoquer tout le monde). Il ne faut pas céder à l’incroyable pression qu’on va vous mettre pour que vous releviez artificiellement vos notes, à la tentation toujours présente de donner des exos triviaux, etc… De toute façon il faut se battre tout le temps… En appliquant cette politique vous aurez les parents sur le dos, la direction le plus souvent (enfin ça dépend), parfois même une partie de vos collègues… mais curieusement vous aurez le respect de vos élèves si vous leur montrer que vous ne voulez pas les brimer mais que vous vous épuisez pour qu’ils progressent. Mais il faut être lucide : vous ne changerez pas le monde à vous tout seul.
Encore une chose, car je ne voudrais pas laisser croire que je me pose en donneur de leçons. Ce que je viens de dire demande beaucoup de courage, et ce courage m’a souvent fait défaut. Et d’autres y arrivent peut-être par des moyens différents, chacun son style.
C’est stupéfiant…. Bien que n’enseignant pas dans l’éducation nationale, j’ai moi aussi constaté des carences de logique et culturelles qui ont une fâcheuse tendance à s’accroître…. Il n’y a qu’une chose à dire : courage aux professeurs, l’éducation doit tenir bon, même si la période n’est pas facile….
Je suis d’accord avec Fabien Besnard, en terminale il est difficile de rattraper un tel retard. Il faudrait y consacrer eu moins un trimestre car il s’agit de plusieurs années d’enseignement non-assimilé au collège — et pour cela le temps manque en terminale.
Les méthodes proposées par lui sont les seules que je vois; on essaye de sauver qui on peut (et qui veut) par quelques cours de soutien, mais il est évident que ce rafistolage est très insatisfaisant, au moins pour le professeur (les élèves ne le ressentent pas tous car ils ont déjà pris l’habitude de l’à-peu-près).
Je trouve ce débat intéressant mais un peu schizophrène. Vous êtes pour la plupart professeur de mathématiques
et vous avez tous l’air de dire que si le niveau a diminué de façon aussi dramatique c’est la faute du système, des élèves qui sont trop nuls. Tout ça est certes vrai, mais ne pensez vous pas que en tant que profs vous faites partie de ce système et j’ai même envie de dire que vous Faites le système? Le retard remonte du collège mais dans ce cas c’est la faute à qui ? c’est la faute aux professeurs de collège ? aux élèves ?
IL va bien falloir qu’à un moment de leur parcours quelqu’un aie le courage de dire » moi je vais à contrepied du programme et je leur apprends ce que je pense être nécessaire et fondamentale » Au lieu de ça les profs de fac disent ils auraient pas du avoir leur bac ( ils l’ont eu grâce à un jury de professeurs non ? ) et les profs de Tle disent ils auraient pas du passer le collège.
D’où ma remarque du début .
Personnellement je pense qu’on devrait revenir aux méthodes anciennes. A force de tout passer aux élèves et d’alléger le programme ils se relâchent eux même et d’autant plus qu’il y’ a beaucoup de personnes prêtes à excuser leur incompétence : les parents, les statistiques ( si 40% des élèves sont nuls je rentre dans les normes…),
les ministres qui prônent perpétuellement une refonte du programme. à un moment donné il va falloir dire aux élèves de travailler, il n’y a pas de miracle. Et d’arrêter de faire le culte de la médiocrité.
Bonjour
Je me demande:
1- quel est le lien des difficultés de ces élèves avec la dyslexie?
2- Quelle est la place des notions, sujets des exercices), dans le programme de la terminale: Les notions évaluées sont enseignées au college et au primaire: ceci peut expliquer les erreurs des élèves du terminale.
1- J’utilisé le mot « dyslexie en maths » pour exprimer le fait de ne pas comprendre l’écriture des mathématiques : opérations élémentaires et les notations de base (fraction, parenthèses, le signe =, etc.). Il ne s’agit pas de dyslexie au sens classique (ne pas savoir lire des mots écrits).
2- Oui, il s’agit du programme du collège. Les mathématiques s’enseignent de manière progressive, et les acquis forment une pyramide qui s’écroule si la base n’est plus là. On ne peut pas enseigner le calcul intégral à des élèves qui ne savent pas calculer l’aire d’un rectangle. C’est comme en anglais par exemple, où on doit savoir conjuguer « to be » sinon ça n’a pas de sens d’analyser un texte de Shakespeare en terminale.
Mais ce n’est pas pareil pour toutes les matières. En Histoire-Géo, par exemple, c’est différent; vous pouvez comprendre assez bien l’Europe du 19e siècle sans connaître la Chine du 5e siècle.
Bonjour
Parfaitement d’accord avec vous sur le 2ème point. Mais ce qui est enseigné n’est parfois acquis que quelques jours, mois et parfois même des années après. Donc (dans un système scolaire) on ne peut pas attendre à ce que tout ce qui est de base soit acquis pour passer à autre chose, L’enseignant (représentant du système scolaire en classe) travail avec le moyen et avance dans le programme qu’il est OBLIGE de terminer en fin d’année.
Le mot que vous avez chisie dysl en maths exprime bien ce que vous avez expliqué.
C’est un article en lien avec la dysl en maths
http://www.ccdmd.qc.ca/correspo/Corr3-4/Math.html
Bonjour à tous,
Sans être professeur de maths , je m’intéresse à tous ces problèmes ne serait-ce qu’en tant que parent d’éleve. On impute souvent les lacunes et le niveau qui baisse en maths ou dans d’autres domaines aux enfants qui ont changé, aux sollicitations du monde extérieur qui détourneraient les enfants des rigueurs de l’apprentissage scolaire, au difficultés sociales etc…Tout ceci joue bien sûr, Il me semble tout de même que les choix politiques et les errements en termes de programme et de choix pédagogiques ont une lourde part de responsabilité dans la situation actuelle.
Cordialement
Anton
Bonjour,
Je viens avec retrad de lire votre excellent article.
etant sortie du lycée depuis un certain teps, j’avoue ne pas avoir été jusqu’au bout de la simplification d’équation ou du calcul sur les droites.
Pour ajouter au débat, j’aime les mathématiques mais lorsqu’elles me sont expliquées d’un façon concrète : je n’ai jamais eu de problème avec des mathématiques financières appliquées mais n’ai jamais pu résoudre de systèmes d’équations linéaires où ne figuraient aucun chiffre.
A mon sens, le problème vient aussi de là : il est difficle de comprendre quelque chose qui est terriblement abstrait et dont on ne voit pas à quoi il sert concrètement (qui à part des ingénieurs et encore résoud des équations sur les droites?).
Ceci dit, merci à mon professeur de mathématiques de 4° qui m’a justement permis d’apprendre les bases de l’algèbre.
Vraiment bon article, ca sert bien.
J’ai d’ailleurs trouvé un site très intéressant pour tous les Bac L qui pourraient passer par là, il s’agit de la communauté des Bac L, avec des cours etc..
L’adresse c’est : bac-L.net
Dites moi ce que vous en pensez !
professeure de mathématiques en Belgique , je vous confirme que ces erreurs traversent les frontières !
Un commentaire pour expliquer la différence entre tête bien pleine et bien faite (je partage l’opinion de Benoît). Les tables de multiplication sont apprises par coeur en primaire. Et au collège, les élèves doivent apprendre et non comprendre que 2(x+2)=2*x+2*2. Peu importe que l’on considère la notion comme triviale et donc comme tant un simple rappel au collège.
Si l’enseignement des tables se faisait avec souplesse et valorisait celui qui ne connait pas ses tables in extenso par cœur mais obtiendrait 5*7 par 25+10, le reste serait alors une formalité.
Le mécanisme de compréhension de la notion de proportionnalité (représentant 80% des notions utiles jusqu’en terminale) s’allume en fait dès le CP, mais est "éteint" par des programmes et des enseignant trop premier degrés dans leur application des programmes. C’est a dire trop pressés d’un coté (progrès mesurables quantitativement), et trop lents de l’autre (établissement de schémas de compréhension).
Pour conclure, quand on ne fait pas confiance en la comprenette des élèves en voulant leur inculquer des réflexes artificiels, il ne faut pas s’étonner qu’ils ne fassent pas confiance eux même en leur propre intelligence. Les profs qui s’offusquent ensuite peut alors sembler une attitude compréhensible alors qu’elle n’est qu’une solution de facilité qu’ils ont mis en place pour ne pas devenir fous face aux absurdité qu’un programme normalisant impose.
Je rajouterais qu’on comprend alors mieux pourquoi de bons élèves (CF notes obtenues) en faculté de sciences sont obligés de poser dans un tableau de proportionnalité les données d’un problème qui se fait de tête.
(mes exemples ne sont évidement que des exemples au même titre que les erreurs rapportés dans l’article de Mathoman ne sont parfois que de simples erreurs d’étourderie au milieu d’erreurs plus graves)