SO(3) e(s)t l’espace projectif à 3 dimensions
Quelques fois on garde un souvenir très complet d’une démonstration mathématique, et ce souvenir inclût également des accessoires absurdes et inutiles comme par exemple le numéro de la page du livre où on l’a apprise ou la couleur de la chemise du professeur qui l’a expliquée…
Ci-dessous j’explique, en forme d’exercice corrigé, pourquoi le groupe SO(3) de rotations dans l’espace peut être identifié à l’espace projectif réel \(\mathbb{P}^3\). Et je me rappelle que c’était un collègue d’études qui m’a raconté cette preuve par la méthode de hand waving sous le soleil d’été dans une piscine plein air à Bonn!
Un bel énoncé géométrie et topologie
Le but de l’exercice est de montrer que \(\;SO(2)\:\simeq\: \mathbb{P}^1\;\;\) et \(\;\;SO(3)\:\simeq\:\mathbb{P}^3\,.\)
Notations
Dans un premier temps — dont nous nous contentons ici — le symbole \(\:\simeq\:\) signifie simplement qu’il existe une bijection entre les ensembles concernés; c’est clairement une relation d’équivalence.
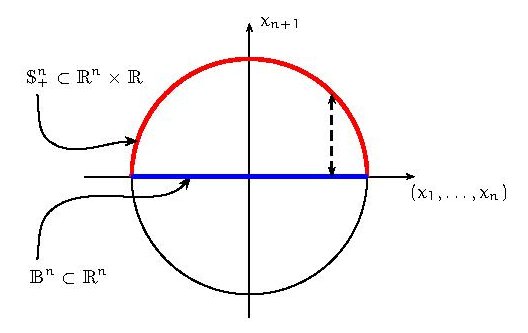
Comme d’habitude \(\mathbb{P}^n\) dénote l’espace projectif réel de dimension n, c’est-à-dire l’ensemble des droites vectorielles dans \(\mathbb{R}^{n+1}\). Fixons aussi les notations pour trois sous-ensembles importants de \(\mathbb{R}^{n+1}\:\):
- la boule \(\;\mathbb{B}^{n+1}=\{x\in\mathbb{R}^{n+1} \:|\: x_1^2+\cdots+x_{n+1}^2\leq1\}\,,\)
\(\:\) - la sphère \(\;\mathbb{S}^{n}=\{x\in\mathbb{R}^{n+1} \:|\: x_1^2+\cdots+x_{n+1}^2=1\}\,,\)
\(\:\) - l’hémisphère nord \(\;\mathbb{S}^{n}_+=\{x\in\mathbb{S}^{n} \:|\: x_{n+1}^2\geq0\}\,.\)
\(\:\)
Le bord de la boule \(\mathbb{B}^{n+1}\) est la sphère \(\mathbb{S}^n\). Chaque point x sur ce bord possède un antipode, à savoir le point —x.
Si on « recolle » \(\mathbb{B}^{n+1}\) par identification des antipodes sur son bord, alors on obtient un nouvel ensemble que nous notons \(\mathbb{B}^{n+1}/\!\sim\,.\) Ca, c’est du handwaving. De manière ensembliste on pourra écrire
\(\;\;\;\;\;\mathbb{B}^{n+1}/\!\sim~\;\,=\;\,\left(\mathbb{B}^{n+1}\backslash\mathbb{S}^n\right)\:\dot{\bigcup}\:
\big\{\{x,-x\}\,|\,x\in\mathbb{S}^n\big\}\,.
\)
Questions
- Expliquer par des mots de quelles formes sont la boule \(\mathbb{B}^n\) et son bord \(\mathbb{S}^{n-1}\) dans les cas n=1,2,3.
- Démontrer que \(\;\mathbb{S}^n_+ \:\simeq\: \mathbb{B}^n\,.\)
\(\,\) - Démontrer que \(\;\mathbb{B}^n/\!\sim~\;\simeq\:\mathbb{P}^n\,.\)
\(\,\) - Démontrer que \(\;SO(2)~\simeq~\mathbb{P}^1\,.\)
\(\,\) - Démontrer que \(\;SO(3)~\simeq~\mathbb{P}^3\,.\)
\(\,\)
Cliquez pour lire la Solution.


De la géométrie différentielle dans un blog ! Chouette 🙂
En fait, cette preuve de SO(3)=P^3 montre seulement une bijection. Mais comme vous le savez, avec un peu plus de travail (ou intuition) on voit que cette bijection est également un isomorphisme dans la catégorie des espaces topologiques — et même dans la catégorie des variétés différentiables, et donc finalement c’est bien de la géométrie différentielle, comme vous le dites.
D’ailleurs pour votre blog je dirais : « Autant d’algèbre et de conseils LaTeX dans un blog ! Chouette 😉 »
tres poussé mais interressant
En fait, la relation entre le projectif et les rotations est plus riches encore. Dans le cas de \(\mathbb P^3\), on peut utiliser les quaternions. Les quaternions unitaires forment un groupe \(S^3\) pour la multiplication des quaternions. De plus, l’application
\(q\mapsto r_q\)
où
\(r_q:h\mapsto qh\overline q
\)
est un homomorphisme de \(S^3\) sur le groupe des rotation de l’espace des quaternions \emph{purs}, dont une base orthonormée positive est \((i,j,k)\). Le noyau de l’homomorphisme est \(\{-1,1\}\) si bien que \(SO(3)\) est le quotient de \(S^3\) par l’équivalence consistant à identifier les paires de points diamétralement opposés.: c’est donc bien l’espace projectif \(\mathbb P^3\). Les vérifications sont faciles en utilisant la forme polaire des quaternions. L’isomorphisme est un homomorphisme de groupes de Lie (i.e. incluant la structure différentiable).
C’est plus simple en dimension deux et, d’ailleurs amusant, en utilisant cette fois les nombres complexes: une droite passant par l’origine est caractérisée par ses deux intersections avec le cercle unité, qui sont deux nombres complexes unitaires opposés. Leur paire est donc complètement caractérisée par leur carré, qui est un point arbitraire du cercle unité. Ici aussi, on obtient un difféomorphisme.
le groupe fondamental \(\pi_1\(
On peut montrer également que l’espace homogène \(SO(3)/SO(2)\) est homéomorphe à la sphère \(S^2\) et encore plus généralement, l’espace homogène \(SO(n+1)/SO(n)\) est homéomorphe à la sphère \(S^n\), en effet \(SO(n+1)\) opère transitivement sur la sphère \(S^n\)(i.e \(\forall x,y \in S^n \exists \sigma \in SO(n+1)/SO(n)\) tel que \(y=\sigma x\), et le sous groupe de stabilité du point \((0,…,0,1)\) est \(SO(n)\). pas conséquent puisque \(SO(n+1)\) est compact \(S^n\) est homéomorphe à \(SO(n+1)/SO(n).\)
\(\forall x,y\in S^n, \exists \sigma \in SO(n+1)\) tel que \(y=\sigma x\)