Preuve que SO(3) est l’espace projectif à 3 dimensions
Ci-dessus la solution pour l’exercice sur le lien entre groupe de rotation et espace projectif.
Réponses aux questions
- \(\mathbb{B}^1\) est l’intervalle fermé [-1,1] et son bord \(\mathbb{S}^0=\{-1,1\}\) est constitué des deux extrémités.\(\mathbb{B}^2\) est un disque et son bord \(\mathbb{S}^1\) est un cercle.\(\mathbb{B}^3\) est une « vraie » boule et son bord \(\mathbb{S}^2\) est une « vraie » sphère.
\(\;\) - Les deux applications suivantes sont bijectives car inverses l’une de l’autre.
\(\;\)
\(
\mathbb{B}^n\:\longrightarrow\:\mathbb{S}^n_+\;,\;\;\;(x_1,\ldots,x_n
)\:\mapsto\:\big(x_1,\ldots,x_n,\sqrt{1-x_1^2-\ldots-x_n^2}\:\big)\,,\)\(\mathbb{S}^n\:\longrightarrow\:\mathbb{B}^n\;,\;\;\;(x_1,\ldots,x_{n+1})\:\mapsto\:(x_1,\ldots,x_n)\,.
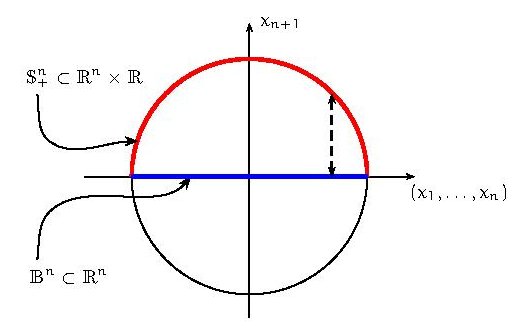
\)Illustration: si on projette l’hémisphère nord sur l’hyper-plan équatorial, on obtient la boule d’unité dans cet hyper-plan.
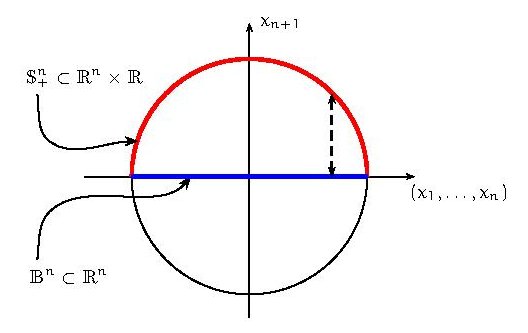
Notons que dans le graphique l’axe des abscisses représente l’espace \(\mathbb{R}^{n}\:\). Il est instructif de comprendre ce dessin déjà pour les plus basses dimensions:
- Si n=1 alors on est dans le plan euclidien \(\mathbb{R}^2\). Le demi-cercle supérieur \(\mathbb{S}^1_+\) (en rouge) se projette bijectivement sur le segment \(\mathbb{B}^1\) (en bleu).
\(\;\) - Si n=2 alors on est dans l’espace plan euclidien \(\mathbb{R}^3\) et \(\mathbb{S}^2\) est une « vraie » sphère dont le dessin montre une coupe. L’hémisphère nord \(\mathbb{S}^2_+\) (en rouge) se projette bijectivement sur le disque \(\mathbb{B}^2\) (en bleu).
\(\;\)
- Si n=1 alors on est dans le plan euclidien \(\mathbb{R}^2\). Le demi-cercle supérieur \(\mathbb{S}^1_+\) (en rouge) se projette bijectivement sur le segment \(\mathbb{B}^1\) (en bleu).
- Chaque droite \(D\in\mathbb{P}^n\) coupe la sphère \(\mathbb{S}^n\) en deux antipodes: \(~\frac{x}{||x||}~\) et \(~\frac{-x}{||x||}~\) où \(x\) est arbitraire dans \(D\backslash\{0\}\).
Au moins un des deux points est dans l’hémisphère nord: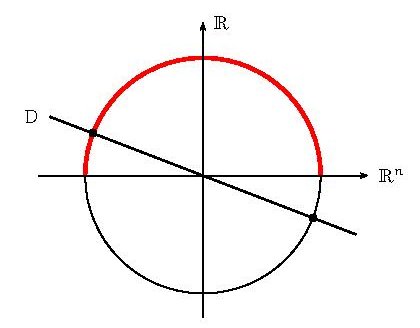
De cette observation on déduit que l’application\(f\;: \;\;\;\mathbb{S}^n_+\;\longrightarrow\;\mathbb{P}^n\:,\;\;\;x\;\mapsto~\mathbb{R}x\,,\)
est surjective; en plus, elle est injective en dehors de l’équateur, et deux antipodes sur l’équateur sont envoyés sur une même image. Plus précisément
\(\forall x,y\in\mathbb{S}^n_+\,:\;\big[\,x\neq y\,\text{ et }\,f(x)=f(y) \:\big]\;\Rightarrow \;
\big[\:x=-y\;\text{ et }\;x_{n+1}=y_{n+1}=0\:\big]\,.
\)Par conséquence \(\: \mathbb{P}^n\: \) est en bijection avec l’ensemble obtenu à partir de \(\: \mathbb{S}^n_+\: \) par identification des antipodes sur l’équateur. Or d’après la question précédente nous savons que \(\: \: \mathbb{S}^n_+ \:\simeq\: \mathbb{B}^n\: \: \) et l’équateur n’est rien d’autre que le bord \(\: \mathbb{S}^{n-1}\: \) de \(\: \mathbb{B}^n\: \). Par conséquence \(\: \: \mathbb{P}^n \,\simeq\: \mathbb{B}^n/\!\sim\: \).
\(\,\)
- Le résultat précédent implique en particulier que \(\:\mathbb{P}^1 \,\simeq\, \mathbb{B}^1/\!\sim\:\).
Or \(\:\mathbb{B}^1\)=[-1,1] et par conséquence \(\:\mathbb{B}^1/\!\sim\:\) est simplement l’intervalle [-1,1] où on a recollé -1 et 1.
Ainsi \(\:\mathbb{B}^1/\!\sim\:\) est en bijection avec le cercle \(\,\mathbb{S}^1\,\). Nous obtenons \(\mathbb{P}^1 \,\simeq\,\mathbb{S}^1\). Illustration: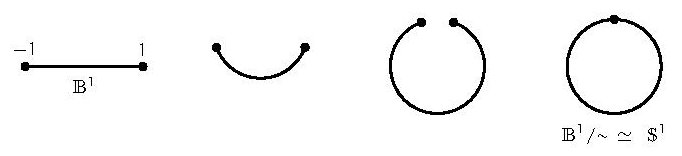
D’autre part \(SO(2)\) est le groupe des rotations du plan euclidien orienté \(\mathbb{R}^2\). Comme chaque rotation est déterminée de manière unique par son angle compris dans \([0,2\pi[\) il est évident que \(SO(2)\) est en bijection avec le cercle \(\mathbb{S}^1\).
Conclusion: \(SO(2)\simeq \mathbb{P}^1\).
\(\,\) - Pour la suite voir le fichier pdf.