Remarques sur l’enseignement des math au collège
Constat : Lacunes dans le post-bac
Il y a quelques semaines, lors d’une colle en prépa MPSI (math sup) sur les développements limités, une étudiante était amenée à calculer la somme de trois fractions,
\(\frac3{40}\;+\;\frac1{12}\;+\;\frac3{8}\;.\)
Voici comment elle s’y prenait (avec mon téléphone portable j’ai pris la photo du tableau) :
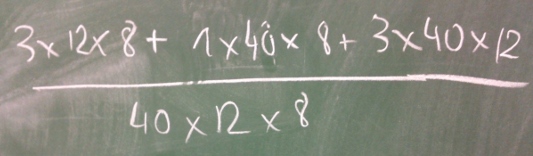 |
|
A éviter : dénominateur inutilement grand
|
Ce qui est gênant dans cette histoire c’est que cette étudiante n’est pas une mauvaise élève, mais apparemment au collège on ne lui a pas enseigné qu’il faut toujours privilégier le plus petit dénominateur commun pour additionner des fractions. En effet, cela évite des grands nombres difficiles à gérer ; le plus petit dénominateur commun n’est pas le produit 40x12x8 des trois dénominateurs ! Il fallait procéder comme suit :
\(\begin{array}{rcl}
\frac3{40}\;+\;\frac1{12}\;+\;\frac3{8} \;&=&\;\frac3{2^3\times5}\;+\;\frac1{2^2\times3}\;+\;\frac3{2^3} \\
\;&=&\;\frac{3\times3}{2^3\times3\times5}\;+\;\frac{2\times5}{2^3\times3\times5}\;+\;\frac{3\times3\times5}{2^3\times3\times5}
\\&&\phantom{\frac{\frac AA}{\frac AA}}\\
\;&=&\;\frac{9+10+45}{2^3\times3\times5}\;=\;\frac{64}{2^3\times3\times5}\;=\;\frac{8}{3\times5}\;=\;\frac{8}{15}
\end{array}
\)
On voit sur la première ligne ci-dessus que le plus petit dénominateur commun est \(2^3\times3\times5\) car c’est le plus petit nombre qui contient
les facteurs premiers qu’on obtient en décomposant chaque dénominateur. Autrement dit, c’est le plus petit commun multiple (PPCM) des trois dénominateurs.
On remarque d’ailleurs que je n’ai pas vraiment calculé
ce dénominateur, je l’ai laissé sous forme de produit car à la fin cela permet de simplifier plus facilement…
Les nombres premiers ont disparu du collège
Comment se fait-il que certains élèves arrivent aujourd’hui en classes préparatoires de sciences et ne savent pas manipuler correctement des fractions ?
La réponse est que la décomposition en produit de facteurs premiers est enseignée beaucoup trop tard et seulement à une partie des bacheliers scientifiques ; en effet, elle n’est plus au programme du collège mais seulement au programme de l’option mathématiques en terminale S.
Il fut une époque en France (pas lointaine et dans autres pays on y est toujours) où tout les enfants apprenaient à l’âge de dix ou onze ans de décomposer un nombre entier en facteurs premiers.
Valeurs pédagogiques et conceptuelles de cette décomposition :
- On apprend à décomposer un
grand problème
enpetits problèmes
, certaines composantes, les nombres premiers, étant irréductibles comme des atomes — ou les briques d’un jeu de légo. - On trouve facilement le PGCD et le PPCM de deux, trois, quatre nombres ou plus à partir de leurs décompositions en nombres premiers. (En revanche, l’algorithme d’Euclid s’applique seulement à deux nombres à la fois.)
- Avec le PPCM on rencontre le concept de la réunion d’ensembles et la signification exacte du mot
ou
. - Avec le PGCD on rencontre le concept de l’intersection et la signification exacte du mot
et
. Ce sont d’ailleurs des notions importantes en probabilités. - On apprend sa table de multiplication…
On se demande vraiment pour quelle raison mystérieuse l’Inspection Générale a-t-elle ôté des programmes le concept simple et fondamental de la décomposition en nombres premiers ? Pour trouver le PGCD de deux nombres elle préconise l’algorithme d’Euclide ! Or cet algorithme est moins intuitif et son fonctionnement plus délicat à comprendre que la décomposition en nombres premiers. Son seul avantage est qu’il marche bien avec les très grands nombres — autrement dit, il n’a aucun intérêt pédagogique… Un jeune esprit a besoin d’apprendre des idées, des concepts et pas quelques recettes pour manipuler de nombres élevés, nombres qui n’ont aucun intérêt, ni pour lui ni pour nous autres mathématiciens (sauf quelques spécialistes en cryptographie, informatique ou théorie des nombres) ! D’abord un enfant doit maîtriser la manipulation des petits nombres, se faire une idée de leurs multiples, de leur diviseurs, et ce défi n’est point gagné à l’époque de la calculatrice…
Supprimer l’enseignement de la décomposition en facteurs premiers était donc une grave erreur et qui plus tard devient source de lacunes ; en plus c’était une occasion manquée de réviser les tables de multiplication.
Plus de vraies constructions géométriques au collège ?
Pour finir, voici deux exemples de l’enseignement actuel de la géométrie, extraits du manuel scolaire Transmath 6e (Nathan 2005). Dans les deux cas l’approximatif remplace une idée de construction simple et précis :
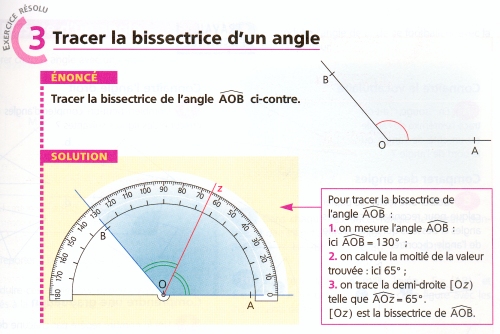
Bissection d’un angle. On ne fait plus appel à la symétrie !
 |
|
Bissectrice — méthode approximative avec pauvre valeur pédagogique
|
Encore une fois, une belle idée conceptuelle est remplacée par un procédé rapide qui n’a pas de valeur pédagogique, comme s’il s’agissait de faire croire aux enfants que plus tard dans la vie ils seraient amenés quotidiennement à diviser des angles ! Or ce qui est intéressant dans la division d’un angle par deux, ce n’est pas le résultat lui-même mais la manière dont on l’obtient, à savoir par un simple concept, la symétrie : si je fais la même construction des deux côtés d’un angle alors j’obtiens une figure symétrique.
Voici donc la vraie construction avec règle et compas telle qu’elle devrait être enseignée :
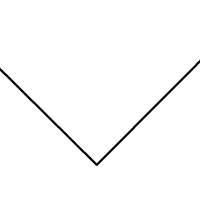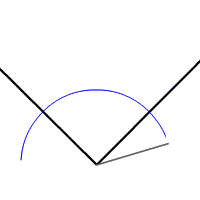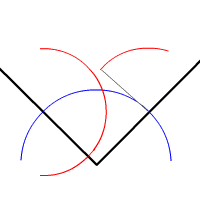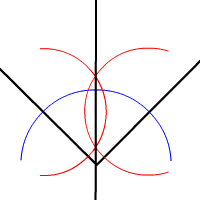 |
|
Bissectrice — la vraie construction intéressante
|
Parallèle à une droite. En appliquant la bissection d’un angle au cas particulier de 180° on obtient une perpendiculaire ; et en faisant la même chose à cette perpendiculaire on trouve une parallèle. C’est une idée simple et facile à retenir. Mais qu’est-ce qu’on enseigne à la place ? La construction approximative que voici :
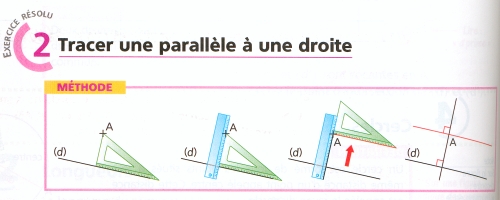 |
|
Parallèle passant par un point — méthode avec peu d’intérêt
|

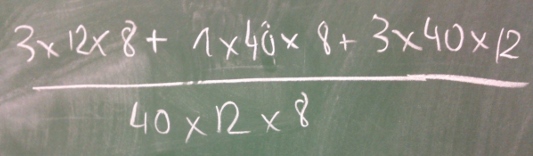
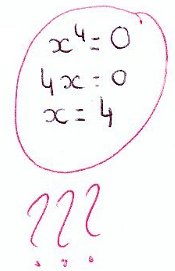

C’est vrai que la construction de la parallèle avec la règle et l’équerre c’est approximatif et tout le monde en terminale ne sait pas encore le faire ! Sans compter ceux qui font "à peu près" avec les deux côtés de la règle…
Il est vrai que l’on nous apprend souvent des petites recettes qui marchent bien mais que les vrais concepts de base sont simplifiés à l’extrême pour soi-disant être plus à notre portée mais on leur enlève tout leur intérêt.
La vraie raison n’est-elle pas que l’élève a eu la flemme de réfléchir à la simplification de cette somme de fractions considérant que cela n’est pas essentielle à la résolution de son problème ?
Autre chose, je ne vois pas en quoi la construction à la règle et à l’équerre d’une paralelle est approximative.
Enfin la construction à la règle et au compas de la bissectrice d’un angle est encore au programme des sixième ou du moins est encore enseigné par les professeur.
http://www.clg-longchamp.ac-aix-...
Se rendre compte qu’une méthode est moins efficace qu’une autre fait aussi partie de l’apprentissage. Aller droit au but sur les techniques les plus efficaces sans trébucher ni tester laisse trop souvent croire que les mathématiques sont figées, indiscutable, inamovibles. Or c’est tout le contraire de cette discipline puisqu’elle laisse la porte ouverte à l’imagination si tant est que l’on donne le temps à l’élève de découvrir et s’intéresser.
Les nombres premiers sont bien évidemment les briques élémentaires par lesquels il faut commencer. Malheureusement la bonne vieille arithmétique à papa n’est plus au programme aujourd’hui.
Elle est remplacée par un cours *super pédagogique* à base d’exercice sur ordinateur avec correction par un simple clic.
Ouaouh la grande classe !
Cordialement
Anthony (un vieux reac de 28 ans ;o)
Je suis tout a fait d’accord qu’il est anormal que la decomposition en produit de facteurs premiers ne soit plus au programe. Le pire, d’apres de que je crois comprendre, est que beaucoup de professeurs de college sont du meme avis mais se sentent obliges de respecter le programme.
Pour ce qui est des constructions a la regle et au compas, mon avis est plus mitige. Quand j’etais eleve au college, je ne comprenais pas pourquoi les profs faisaient des constructions si compliquees pour trouver le milieu d’un segment, alors qu’il suffit de mesurer le segment et de diviser la longueur pas 2. Mathoman a l’air de dire que c’est une construction approximative, mais les graduations d’une regle sont-elles reellement moins precises que la pointe du compas (qui a une epaisseur non nulle)?
Quand j’ai commence a preparer quelques etudiants a l’agregation il y a quelques annees, il y avait une lecon "constructions a la regle et au compas", ou on pouvait disserter sur certains problemes qui ont inspire les mathematiciens pendant des siecles (problemes de la quadrature du cercle, de la trisection de l’angle, etc.). On pouvait raconter que l’ensemble des nombres complexes constructibles est le plus petit sous-corps de C contenant Q et stable par racine carree et, moyennant un peu de theorie de Galois, montrer que le polygone regulier a 17 cotes est constructible, ce qu’avait deja etabli Gauss 35 ans avant que la theorie de Galois ne soit connue… puis la lecon a disparu du programme de l’agregation. Pourquoi? Peut-etre parce que son contenu etait un peu trop previsible… ou bien est-ce parce que ca n’apporte pas grand chose au reste des mathematiques ni aux autres sciences des savoir effectuer des constructions a la regle et au compas?
P.S. Sur le site de SLECC (savoir lire, écrire, compter, calculer), on peut lire un texte du GRIP (Groupe de Réflexion Interdisciplinaire sur les Programmes) contenant une proposition de programme pour l’école primaire :
http://www.slecc.fr/programmes_g...
En page 7, ils proposent d’enseigner les notions de nombre premier et décomposition d’un entier en nombres premiers, ainsi que les notions de PGCD et de PPCM aux élèves de cours moyen (CM1, CM2).
Il ne reste plus qu’à attendre qu’un ministre de l’éducation nationale raisonnable apprécie le travail effectué…
La vraie raison n’est-elle pas que l’élève a eu la flemme de réfléchir à la simplification de cette somme de fractions considérant que cela n’est pas essentielle à la résolution de son problème ?
Non. En fait, les fractions de la somme sont déjà simplifiées, c’est seulement en les réduisant au même dénominateur qu’elle n’utilise pas la bonne démarche, et cela simplement car elle ne la connaissait pas. C’est normal, il ne faut pas s’attendre à ce que les élèves ré-inventent la roue.
A mon avis, dans dix ou vingt ans quelqu’un dans l’Inspection Générale « rédecouvrira » les nombres premiers et les mettra au programme comme quelque chose de « très original et ludique »…
Autre chose, je ne vois pas en quoi la construction à la règle et à l’équerre d’une paralelle est approximative.
Mathoman a l’air de dire que c’est une construction approximative, mais les graduations d’une regle sont-elles reellement moins precises que la pointe du compas (qui a une epaisseur non nulle)?
Là, je suis d’accord avec vous ! C’est au moins aussi précis que la construction classique.
Aller droit au but sur les techniques les plus efficaces sans trébucher ni tester laisse trop souvent croire que les mathématiques sont figées, indiscutable, inamovibles.
Aussi d’accord.
Je ne veux préjuger de rien, mais accuser l’enseignement primaire me parait aller un peu vite en besogne.
Je me souviens d’une expérience personnelle où, arrivé en terminale S, moi et mes camarades de promo, nous avions oublié comment se faisait une division Euclidienne. Pourtant nous n’étions en rien des cancres en mathématiques et nous avons connu les "anciens" programmes (j’ai appris les nombres premiers en CM2). Le fait est que nous avions tout simplement oublié par manque de pratique. Il a simplement fallu qu’une prof nous en fasse gentiement la remarque, pour que nous nous replongions sur son fonctionnement.
Selon moi crier au scandale en affichant fièrement une photo de son incapacité (ou de son oubli, ce que je pense) me semble contre productif et pire, risque de la braquer si par mégarde elle tombe dessus. Un simple rappel devrait suffir.
Peut-être je n’étais pas assez clair. Je disais que l’étudiante en question n’est pas mauvaise mais qu’elle ne manipule pas correctement les fractions car elle n’a jamais vu de factorisation en nombres premiers — et que ce n’est pas de sa faute car ce n’est plus au programme (je ne lui ai pas donné une mauvaise note de colle, je lui ai expliqué comment la factorisation fonctionne, puis j’ai demandé si je pouvais prendre la photo pour mon site). Ce n’est donc pas un oubli mais bien l’erreur de l’enseignement actuel au collège. On peut d’ailleurs constater la même chose pour le programme de maths au lycée où on fait un peu de tout mais peu de bien (zapping). Or je pense qu’en pédagogie mathématique on a
1 + 1 > 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2.
Désolée mais cette étudiante a forcément vu la décomposition d’un entier en produit de facteurs premiers puisqu’elle était au programme des classes de seconde encore en vigueur l’an dernier.( voir le BO hors série du 30/08/2001 )
Elle l’a donc vue et a fait quelques exercices ( simples ) d’application il y a 3 ans…et elle a oublié car depuis elle a toujours utilisé sa calculatrice pour rendre une fraction irréductible
Profm : si elle avait appris la décomposition en facteurs premiers en quatrième et non en seconde, elle aurait beaucoup pratiqué apprenant un an plus tard le calcul des fractions et elle n’aurait sans doute pas oublié.
je suis prof en collège depuis 1990.
Au début, la décomposition était enseignée.
Depuis plusieurs années, elle n’est plus du programme (les tête pensantes ne pensent pas toujours à tout !!!). Mais, nous avons à la place les probabilités (enfin quelques notions de bases sur les expérience aléatoires)
Par contre, la construction de la bissectrice d’un angle au compas est toujours au programme de 6° (comme axe de symétrie d’un angle);
De plus, la construction de parallèles au compas est du programme de 5° (avec les parallélogrammes)
Merci pour ces précisions !
Je mentirais si je disais que ce genre d’article me rappel de bons souvenir de ma scolarité, je n’étais pas très fan des mathématiques…