Une preuve à prendre avec précaution
Le fait que
est une des premières choses qu’un étudiant apprend lorsqu’il étudie les nombres réels. Voici une démonstration
de cette égalité.
On pose
X = 0,99999…Alors on a l’égalité
10X = 9,99999…dont on soustrait la première,
9X = 9,00000…D’où X = 1.
Convaincant, n’est-ce pas ? Pour beaucoup de gens il s’agit d’une preuve
— mais en réalité ça reste une tricherie car on ômet de réfléchir sur un certain nombre détails (comme par exemple à la signification rigoureuse de 0,99999… ou du produit 10 × 0,99999…. C’est un peu comme en topologie où il faut aussi faire comprendre au débutant que le fait que les boules ouvertes sont des ouverts nécessite une preuve.)
Or qui a bien compris le cours sur les nombres réels n’a pas besoin d’une preuve car l’égalité 0,999999… = 1 est une conséquence immédiate des diverses définitions possibles du corps des réels.
Voici la manière dont j’expliquerai l’égalité 1=0,99999… à quelqu’un qui ne connais pas grand chose en maths :
Une bien meilleure méthode
On pose X = 0,99999… et on part de
0 < 0,9 < 0,99 < 0,999 < 0, 9999 < … < X
donc par multiplication par -1 les inégalités changent de sens,
0 > – 0,9 > – 0,99 > – 0,999 > – 0,9999 > … > – X.
En ajoutant 1 à chaque membre de ces inégalités, on obtient
1 > 1 – 0,9 > 1 – 0,99 > 1 – 0,999 > 1 – 0,9999 > … > 1 – X.
Autrement dit,
Ainsi la différence 1-X est plus petite que tout nombre de la forme 0,000…0001. C’est-à-dire 1-X ne peut pas être strictement positif. D’autre part 1-X n’est pas strictement négatif car X n’est pas plus grand que 1. Cela prouve que 1-X = 0 , ou encore que X = 1. CQFD
Avec un tel raisonnement, je crois, le non-initié comprend mieux les idées mathématiques qu’avec une tricherie qui fait seulement appel à ses habitudes de calcul.
Brenoms
D’ailleurs au lieu d’écrire une infinité de chiffres après la virgule on peut aussi écrire une infinité de chiffres devant. On obtient alors ce qu’on appelle un brenom (verlan de nombre). On additionne les brenoms en commencant par la droite. Ca donne des résultats bizarres comme par exemple
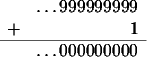
Plus de détails sur les brenoms dans ce bel article.



Bonjour / bonsoir,
étant un nouveau dans le monde fantastisque des maths post-bac, j’ai effectivement rencontré cette preuve assez étrange au premier abord, par un camarade. Puis notre professeur nous a expliqué le pourquoi du comment et en a même profité pour nous donner une méthode de démonstration mettant en jeu les notions de sommes finies que nous venions de voir (avec en supplément un passage à la limite qui n’était pas dans le chapitre). Et pour les plus sceptiques, je me propose de la restituer (par contre, j’espère que ces sceptiques connaissent leur formule de la somme des termes d’une suite géométrique… ce qui est assez anecdotique par rapport au changement de variable).
Alors d’abord pour des commodités d’écriture, j’utiliserai la notation \(0,\bar{9}\) pour désigner \(0,9999\cdots\)
Alors \(0,\bar{9}=\displaystyle{\sum_{k=1}^{+\infty}9.10^{-k}=\lim_{N\to +\infty}\sum_{k=1}^{N}9.10^{-k}}\)
Or \({\displaystyle \sum_{k=1}^{N}9.10^{-k}=9.\sum_{k=1}^{N}10^{-k}=9.\sum_{k=1}^{N}\left(\frac{1}{10}\right)^{k}=9.\sum_{k=0}^{N-1}\left(\frac{1}{10}\right)^{k+1}=\frac{9}{10}.\sum_{k=0}^{N-1}\left(\frac{1}{10}\right)^{k}}\)
Et \({\displaystyle \sum_{k=0}^{N-1}\left(\frac{1}{10}\right)^{k}=\frac{1-\left(\frac{1}{10}\right)^{n}}{1-\frac{1}{10}}=\left(1-\left(\frac{1}{10}\right)^{n}\right).\frac{10}{9}}\)
Donc \({\displaystyle \sum_{k=1}^{N}9.10^{-k}=\left(1-\left(\frac{1}{10}\right)^{n}\right)}\)
Finalement, avec le passage à la limite, \(0,\bar{9}=1\).
Si c’est discutable au niveau topologie ou autre, je ne pourrai pas améliorer, je ne suis pour l’instant qu’à mon premier trimestre de maths sup ^^’
En tout cas le réseau de blogs de maths propose des articles très intéressants. Merci de votre attention.
Voici un argument qui n’est pas du tout une demonstration mais qui me semble avoir l’interet d’etre convaincant pour le profane.
On sait que 1/9 = 0,11111…
En multipliant par 9 on trouve :
1= 0,99999…
@ JLT : Est-ce que toute monde sait que 1/9 = 0,11111… ? 😉
@ Alexandre : Oui, c’est une bonne preuve de passer par la série géométrique (pour ceux qui la connaissent). Je viens de rajouter au billet la preuve qui me paraît le mieux adaptée pour des non-matheux.
Sincèrement je trouve la seconde preuve très obscure pour un profane même si effectivement elle est rigoureuse. Les matheux font en permanence des racourcis dans leurs preuves, et heureusement car si nous rédigions toutes nos preuves en utilisant les axiomes de la théorie des ensembles nous ne serons pas sorti de l’auberge…
Pourquoi alors imposer à quelqu’un qui ne connait les maths que de façon parcellaire un raisonnement si compliqué. Perso, je garde le premier raisonnement pour les novices et je creuse d’avantage pour les étudiants.
Salut Bernhard,
Je suis, comme tu le sais, un profane (je n’ai pas fait de maths depuis le bac, donc depuis presque 20 ans) mais j’aime bien la logique.
La preuve n°1 (où l’on triche) m’a quand même paru la plus simple à comprendre. Encore que je ne suis pas sûr d’avoir tout compris. Pour les autres démonstrations, il faut réfléchir plus. C’est fatiguant.
Tu as raison de signaler cette arnaque que l’on trouve dans certains livres de seconde. Il se trouve que j’ai eu à enseigner en classe de seconde (quelques uns s’en souviennent peut-être avec douleur). Pour expliquer que 0,999…=1, je partais des deux faits suivants (admis) : tout nombre réel admet un développement décimal, entre deux réels distincts il s’en trouve toujours un troisième. Puis je raisonnais par l’absurde en cherchant le développement décimal d’un nombre qui serait coincé entre 0,999… et 1,000… Bien sûr cela revient exactement à ta preuve, mais c’est peut-être un peu plus intuitif.
Pouvez-vous expliciter pour moi, en termes simples votre remarque "C’est un peu comme en topologie où il faut aussi faire comprendre au débutant que le fait que les boules ouvertes sont des ouverts nécessite une preuve"?
J’avoue ne rien comprendre tout en étant à la fois mathématicien et pédagogue…
C’est assez simple à comprendre. Soit (X,d) un espace métrique (par exemple Rn avec comme métrique la distance habituelle (euclidienne) entre deux points.)
Pour a dans X et r>0 on appelle « boule ouverte » de centre a et rayon r l’ensemble Br(a) constitué des x dans X tels que d(x,a)<r.
On définit qu’une partie Y de X est « ouverte » si pour tout y dans Y il existe r>0 tel que Br(y) est une partie de Y. On on déduit sans problème que les ouverts de X forment une « topologie » sur X, c’est-à-dire que X et l’ensemble vide sont ouverts, que toute réunion d’ouverts est un ouvert et que toute intersection finie d’ouverts est un ouvert.
Mais ce qui n’est pas évident c’est que les « boules ouvertes » portent bien leur nom et sont des ouverts dans cette topologie. La preuve de ce fait n’est pas difficile (elle fait appel à l’inégalité triangulaire, l’un des quatre propriétés qui définissent une métrique) mais sa nécessité étonne les étudiants…
Bonjour,
On m’a parlé de cette égalité il y a longtemps déjà, mais je n’arrive pas à m’y résoudre. Je suis pas un mathématicien, mais en regardant les différentes démonstration, je trouve à chaque fois des éléments qui me semblent litigieux (voir ci après). Alors si vous pouvez me dire ce qui cloche dans mes raisonnements !
1) D’un point de vu du vocabulaire, admettre que 0,999… = 1 revient donc à dire que l’infini est égal au fini, or, les définitions usuelles (Larousse) des termes infini et fini sont très clairement contraires….
2) Démonstration 1/3 = 0,333…
1/3 = 0,333…
3 * 1/3 = 3 * 0,333…
1 = 0,999…
Points litigieux
– Est ce que 1/3 = 0,333… ? Car en admettant cela on admet ce que l’on veut démontrer !
On peut en effet considérer que 0,333… n’est pas à proprement parler égal à 1/3, mais plutôt une valeur approchée qui ne l’atteint jamais, puisque infini (de même que 1 serait une valeur approchée de 0,999…).
S’il s’agit d’une approximation, il en va de même avec le résultat final.
– Par ailleurs, on peut se demander comment multiplier un nombre fini avec un nombre infini à un sens ?
3) Démonstration x = 0,999…
x = 0,999…
10 * x = 9,999…
10 * x – x = 9,999… – x
9 x = 9,999… – 0,999…
9 x = 9
x = 1
0,999… = 1
Points litigieux
– Ici encore on peut se demander comment multiplier un nombre fini avec un nombre infini à un sens ?
En effet, dire que 10 * 0,999… = 9,999… est litigieux car, si l’on considère que
d’un côté
10*0,999… = 0,999… + 0,999… + 0,999… + 0,999… + 0,999… + 0,999… + 0,999… + 0,999… + 0,999… + 0,999…
et que de l’autre
9,999… = 9 + 0,999… = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 0,999…
On serait tenté de dire que l’on a discrètement remplacer neuf 0,999… gênants par des 1 puis, par un tour de magie, fait disparaître le dernier 0,999…. On en revient à la démonstration passant par 1/3 en admettant ce que l’on souhaite démontrer au lieu de le démontrer.
Est-il donc réellement possible d’utiliser la multiplication et soustraction sur des valeurs infinies ?
4) Démonstration des réels différents
Or, on ne peut pas intercaler de nombre entre 0,999… et 1 ; ils sont donc égaux.
Points litigieux : Dire que l’on ne peut pas intercaler de nombre entre 0,999… et 1 ressemble plus à une affirmation qu’à une démonstration
5) Démonstration suite géométrique et limites
Sans reprendre la démonstration présentée plus haut, l’élément qui me dérange c’est que, si j’ai bien compris, la somme d’une telle suite TEND vers une limite. La limite peut donc bien être égale à 1 sans pour autant qu’on l’atteigne ou que l’on puisse l’atteindre ! Une fois de plus, il me semble que l’on en revient à approximer le résultat par sa limite, mais pas à prouver que c’est une égalité stricte ?
Pour répondre à la dernière question de votre commentaire. L’écriture 0.999… avec une infinité de chiffres n’a pas de sens si on ne dit pas ce qu’elle signifie. L’unique manière de lui donner du sens est justement de lui attribuer la valeur de la limite de la suite 0.9, 0.99, 0.999, …
On peut montrer que toute suite de la forme 0.a, 0.ab, 0.abc, … (où a, b, c, … sont des chiffres entre 0 et 9) converge vers une limite finie.
Quand vous parlez de « nombre infini » vous voulez dire « limite d’une telle suite ayant un nombre infini de chiffres non nuls ».
On peut également considérer que l’écriture 0,99999999… désigne le nombre que l’on obtient en ajoutant 9 dixièmes et 9 centièmes et 9 millièmes et ainsi de suite. Une ambiguïté réside dans la signification de et ainsi de suite. Car plus on va ajouter de décimales, et plus le nombre augmentera, se rapprochant de plus en plus de 1 sans jamais l’atteindre. C’est parce que l’on se rapproche de plus en plus de 1 que l’on peut considérer que 1=0,99999999…. C’est une approche qui est généralement partagée par les mathématiciens pour donner du sens à une écriture décimale infinie.