Une preuve combinatoire
La récurrence est un outil très performant pour démontrer des formules qui dépendent d’un nombre entier. Lorsqu’on l’enseigne on est content si les étudiants en ont compris le principe et savent rédiger correctement une preuve par récurrence. Mais il arrive que des preuves par récurrence sont un peu mécaniques et ont une valeur pédagogique pauvre car elles n’apprennent pas beaucoup sauf à écrire des transformations de termes. Un exemple bien connu est la formule du petit Gauß:
\(1+2+3+\cdots+n=\frac{n(n+1)}2.\)
Bien évidemment une preuve par récurrence est possible et je la fais souvent dans mes cours; mais elle n’est pas belle
et n’apprend pas grande chose au niveau mathématique. Bien évidemment je présente à mes étudiants aussi la méthode utilisée par le petit Gauß à l’âge de neuf ans. On écrit la somme en montant, puis en descendant; on constate que les deux termes qui se trouvent un au-dessus de l’autre ont toujours la somme n+1 :
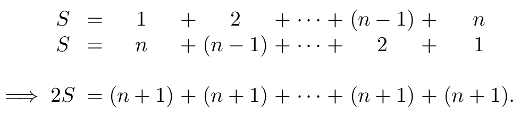
Par conséquence 2S=n(n+1) et la formule est démontrée.
Maintenant je prie mes lecteurs d’aller un peu plus loin en démontrant, toujours sans récurrence, la formule de la somme des nombres cubes:
\(1^3+2^3+3^3+\cdots+n^3=(1+2+3+\cdots+n)^2.\)
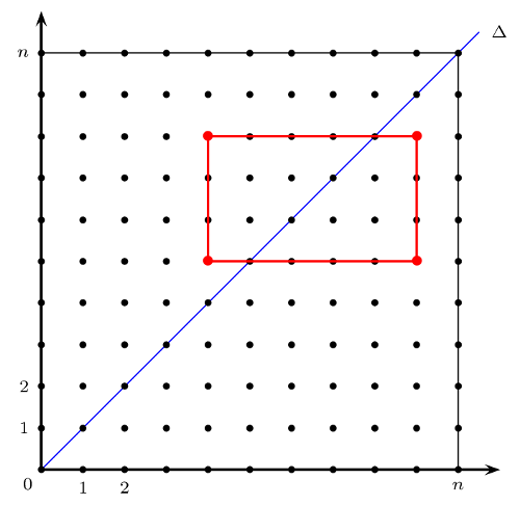
Indication: On pourra dénombrer les rectangles contenus dans la carré \(\llbracket0,n\rrbracket\times\llbracket0,n\rrbracket\) de sorte que les cotés soient parallèles aux axes de coordonnées. Une méthode pour dénombrer consiste à distinguer les rectangles selon la position du sommet nord-est par rapport à la diagonale du carré.
D’ailleurs je serais intéressé de connaître une preuve combinatoire pour la somme des nombres carrés.
Autre remarque: C’est un exercice classique de prépa de déduire de la formule du petit Gauß la formule pour la somme des nombres carrés, puis déduire de la formule de la somme des nombres carrés celle de la somme des nombres cubes, etc. C’est-à-dire, on établit de manière récursive la formule avec exposant r à partir de celle avec exposant r-1.



Je vais utiliser le fait que deux fonctions ayant mêmes dérivées diffèrent d’une constante (sur un connexe, bien entendu, mais cela ne jouera pas ici).
Posons
\(s_n=\sum_{k=1}^nk^3\)
La dérivée de cette suite est
\(s_{n+1}-s_n=(n+1)^3\)
Posons ensuite
\(t_n=(1+\cdots+n)^2\)
La dérivée de cette suite est
\(t_{n+1}-t_n=(1+\cdots+n+1)^2-(1+\cdots+n)^2=(n+1)^2+2(n+1)(1+\cdots+n)\)
Avec la formule du petit Gauss, il vient aussitôt
\(t_{n+1}-t_n=(n+1)^3\)
La conclusion est alors immédiate car \(s_1=t_1=1\).
(La suite \(x_n\) est reconstituée à partir de sa dérivée via
\(x_n=(x_n-x_{n-1})+\cdots+(x_2-x_1)+x_1\))
La même méthode fonctionne très bien pour démontrer la formule du petit Gauss mais aussi … celle de la somme des carrés!
Désolé, ce ne sont pas des preuves combinatoires. Ce sont simplement des preuves sans récurrence.
Merci, Pierre, pour cette preuve. Elle ressemble à la méthode que j’ai mentionnée à la fin.
Voici la preuve combinatoire que j’avais en tête. On dénombre de deux manières différentes les rectangles contenus dans le carré \(\llbracket0,n\rrbracket^2\) et ayant les cotés parallèles aux axes de coordonnées.
La première manière pour déterminer le nombre de tels rectangles est la suivante: Choisir le rectangle revient à choisir deux droites verticales parmi les n+1 droites d’équations x=0,…,x=n et deux droites
horizontales parmi les n+1 droites d’équations y=0,…,y=n. Donc le nombre de rectangles possibles est
La deuxième méthode de dénombrement est un peu plus tordue. On a trois classes de rectangles, selon la position du sommet nord-est par rapport à la diagonale \(\Delta\) d’équation y=x. En fait, ce sommet peut être en-dessous ou bien au-dessus ou bien sur \(\Delta\).
Considérons d’abord le cas où le sommet nord-est est sur la diagonale \(\Delta\). Ainsi il est de la forme (p,p) avec \(1\leq p\leq n\). Il reste alors p2 positions possibles pour le sommet sud-ouest, à savoir toutes les positions dans le carré \(\llbracket0,p-1\rrbracket^2\). Comme le choix de ces deux sommets opposés détermine le rectangle on déduit que le nombre de rectangles possibles avec sommet nord-est sur la diagonale vaut
Maintenant dénombrons les rectangles avec sommet nord-est en-dessous la diagonale. Les deux sommets à l’est sont sur une droite verticale y=p avec \(2\leq p\leq n\). Alors il existe
\({p\choose2}\) choix possibles pour la position de ces deux sommets. Après les avoir choisis il reste p choix possibles pour la position des deux sommets ouest (leurs ordonnées sont déjà imposées). Par conséquence le nombre de rectangles avec sommet nord-est en-dessous de la diagonale est
Par symétrie c’est aussi le nombre de rectangles avec sommet nord-est au-dessus de la diagonale. Ainsi le nombre total de rectangles possibles vaut
\sum_{p=1}^np^2+2\sum_{p=2}^np{p\choose2}&=\sum_{p=1}^np^2+\sum_{p=2}^np^2(p-1)
\\
&=\sum_{p=1}^np^2+\sum_{p=1}^np^2(p-1)\\&=\sum_{p=1}^np^3.
\end{align*}\)
Une comparaison avec le résultat de la première méthode donne la formule souhaitée.