Un peu de combinatoire en cercle
Chaque année, lors des premières colles de prépa math sup en septembre je pose des petits exos en combinatoire élémentaire. Je trouve que ces questions de dénombrement sont instructives le débutant — genre: Pour un conseil de ministres on place n ministres autour d’une table ronde, n>2. Chaque ministre peut discuter seulement avec ses deux voisins. Combien de conseils différents peut-on former?
Voici un autre exercice (un peu plus recherché) de combinatoire sur un cercle. Peut-on placer sur un cercle 2n chiffres 1 ou 0 tel que chaque suite possible de n chiffres 1 ou 0 peut-être lue en partant quelque part sur le cercle?

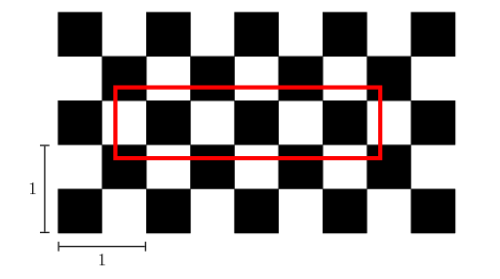
Je sèche !
J’ai bien envie de dire que c’est toujours possible, mais je peine à construire un exemple à partir de \(n=5\)…
Supposant que ce soit effectivement possible (et supposant bien entendu que l’on ne peut lire les nombres que dans un seul sens), chaque séquence possible de \(k\) chiffres (\(1 \le k \le n\)) doit apparaître exactement \(2^{n-k}\) fois. En particulier, les suites de longueur \(n\) apparaissent toutes exactement une fois, et il y a autant de 0 que de 1 (chacun apparaissant \(2^{n-1}\)). On peut également dire qu’il y a une seule suite de \(n\) 1 entourée de 0 et inversement, qu’elles contiennent toutes les suites constantes de longueur \(n-1\), et il y a à part une seule suite constante de longueur \(n-2\) pour 0 et pour 1, etc.
Cela dit je doute fort qu’une preuve par construction soit possible. La non-unicité de la solution (j’ai trouvé au moins deux suites pour \(n=4\)) me fait penser que de telles suites sont peut-être nombreuses, et que l’on peut trouver une borne inférieure sur leur nombre… Mais tout cela est très vague. Tout indice est donc le bienvenu. 🙂
la question de générer toutes les suites de n caractère sur un alphabet à k éléments par permutation circulaire des caractère d’une chaîne peut être vue comme un problème de théorie des graphes (en fait de théorie des langages). Si on représente la situation par un graphe orienté dont :
-les sommets sont les suites de n caractères
-les arcs partent d’une suite de caractères vers celles obtenues en enlevant le premier caractère et ajoutant un caractère quelconque à la fin
le problème revient alors à trouver un circuit Hamiltonien (passant par tous les sommets du graphe). Le graphe devient vite difficile à construire puisqu’il y a \(k^n\) sommets chacun ayant un degré entrant de k et un degré sortant de k, il y a donc \(k^{n+1}\) arc d’après le lemme des poignées de mains.
Concrètement pour un alphabet à 2 éléments {0;1} et si on cherche les suites de n=4 caractères vous aurez des arcs comme (0110)—>(1100) car en ajoutant A à la fin de 0110 on obtient la nouvelle séquence 1100. Au final une solution est donnée par la suite de longueur 16 : 0000101100111101, et le graphe sous-jacent est visible à l’adresse suivante : lh5.googleusercontent.com…
Si tu veux plus d’informations, il faut chercher du coté des suites de De Bruijn, pour k et n données il y a \(\dfrac{\left(k!\right)^{k^{n-1}}}{k^n}\) suites de longueur \(k^n\) donnant toutes les combinaison possible par rotation circulaires :
en.wikipedia.org/wiki/De_…
on trouve ça aussi dans des problèmes pratiques comme le craquage rapide d’un digicode (ça fait un très bon sujet de DS en théorie des graphes!).
La réponse de philippe convient bien pour résoudre le problème mathématique. Je me permet de faire une petite remarque d’ordre algorithmique sur la construction de la solution.
Dans la preuve, tu te ramène au problème du circuit hamiltonien. Or, à moins d’affirmer que P=NP, le coût temporel de la recherche du circuit hamiltonien sera exponentiel, dans le pire cas, en la taille des données. Ici, la donnée est un graphe avec \(k^n\) sommets et \(k^{n+1}\) arcs. L’algorithme complet aura donc un coût en \(O(m^{k^{n+1}})\) pour un certain réel m. Une utilisation pratique de cette algorithme est donc difficilement envisageable.
On peut améliorer la complexité en suivant la même idée de départ. Concernant le graphe, il n’y a qu’une modification: les sommets sont les suites de (n-1) caractères. La différence semble mince mais c’est ce qui permet de se ramener non pas au problème du circuit hamiltonien, mais au problème du circuit eulérien (dont le coût est linéaire en la taille des données). La construction du graphe reste coûteuse puisqu’il y a \(k^{n-1}\) sommets et \(k^n\) arcs.
Une suite de n caractères se représente comme un sommet du graphe associé à une transition sortante. Ainsi, sur 7 caractères, la suite 1234567 sera représentée par le sommet 123456 associé à la transition (123456)–>(234567). La recherche de la séquence voulue nécessite donc de parcourir toutes les arêtes et de revenir au point de départ (ie de trouver un circuit eulérien).
Cet algorithme est en \(O(k^n)\). On ne peut pas faire mieux car la simple construction de la séquence nécessite déjà \(k^n\) lettres.
A tout problème eulérien sur les graphes, on peut lui associer un problème hamiltonien dual. Il suffit de partir du graphe 1 où l’on cherche un circuit eulérien et de construire un graphe 2 (dual du premier) où l’on traitera le problème hamiltonien. Le graphe 2 s’obtient ainsi:
-les sommets représentent les arêtes du graphe 1.
-deux sommets du graphe 2 sont connectés entre eux si les arêtes associées du graphe 1 possèdent une extrémité en commun.
Par exemple, on peut voir que le graphe présenté par philippe est le graphe dual du graphe que je viens d’exposer plus haut.
La connaissance de cette réduction "problème eulérien –> problème hamiltonien" amène certaines questions (dont je ne connais pas les réponses): quand je dois résoudre un problème hamiltonien sur un graphe, puis-je m’assurer que ce graphe n’est pas le dual d’un autre où je pourrais résoudre un problème eulérien ? A partir d’un graphe dual, peut-on retrouver le graphe d’origine rapidement ?
bravo leokent ! C’est vrai que quand on s’est ramené à un problème hamiltonien c’est un bon réflexe d’essayer de se ramener à un problème Eulerien, sachant que c’est pas facile de reconnaitre qu’un graphe soit le dual d’un autre. Comme toi je ne sais pas s’il y a un moyen de caractériser un graphe dual directement …?
Je lis sur le net le joli truc suivant : soient \(K\) un corps à \(2^n\) éléments, \(a\) un générateur du groupe multiplicatif \(K^\times\) et \(f:K\to \mathbb F_2\) une forme linéaire non nulle; alors la suite \((f(a),f(a^2),\ldots,f(a^{2^n-1}))\), à laquelle on ajoute un 0 à un emplacement convenable, est une suite de 0 et de 1, de longueur \(2^n\), qui contient, si on la regarde comme un "cycle", tous les "mots" de longueur n.
Chouette ! J’essaye avec n=3 pour voir : choisissons le corps \(K:={\mathbb F}_2[X]/(X^3+X+1)\), choisssons pour \(a\) la classe de \(X\), et choisissons pour \(f\) la forme linéaire "terme constant". On a immédiatement :
\((1,a,a^2,a^3,a^4,a^5,a^6)=(1,a,a^2,a+1,a^2+a,a^2+a+1,a^2+1)\) et en passant aux "termes constants" on obtient la suite \((1,0,0,1,0,1,1)\). Ajoutons un 0 voisin des deux 0 consécutifs : \((1,0,0,0,1,0,1,1)\). Voilà une suite "cyclique" de longueur 8 qui doit contenir tous les mots de longueur 3.
Une fois le fait général du début démontré, on a un algorithme sympathique pour fabriquer une suite comme demandée (il suffit essentiellement de trouver polynôme "primitif" de degré donné sur un corps premier fini).
Merci pour toute cette participation! Je suis content que cette question ait inspiré PB ce billet sur son blog.