Hand waving et dessins en mathématiques
Les chercheurs en mathématiques appellent hand waving une manière d’expliquer une idée oralement et avec les mains, sans faire appel à un formalisme poussé. Dans certaines situations, cette démarche est justifiée et peut être très efficace.
Si on veut être méchant on pourrait dire que, pour expliquer sa nouvelle découverte un mathématicien a besoin de
- ses mains et 15 minutes s’il s’adresse à un collègue dans la cafétéria de son centre de recherche,
- cinq transparents et 60 minutes s’il l’expose dans un séminaire,
- vingt pages qui demandent trois jours de lecture, s’il la publie dans une revue scientifique.
Le problème est que les mathématiques demandent la précision totale, et celle-ci nécessite un formalisme exacte et sans ambiguïté. Oralement, en faisant des dessins avec les mains dans l’air ou sur un brouillon, on peut toujours guider son interlocuteur et l’empêcher de mal comprendre. Mais ce n’est pas le cas en communication écrite où l’auteur est obligé de traduire ses idées en un formalisme que le lecteur devra ensuite retraduire en idées!
Beaucoup d’énergie est perdue dans ces efforts de traduction et re-traduction. Pour minimiser ces efforts le lecteur doit s’entraîner à maîtriser le formalisme et l’auteur, de son côté, doit inventer un formalisme facile à lire et avec des notations intuitives — et, si possible, ajouter des dessins à son texte!
Malheureusement, dans beaucoup de manuels universitaires, il n’y a pas assez de dessins. Peut-être c’est dû à la paresse des auteurs qui rédigent en LaTeX où il est beaucoup plus rapide d’écrire cinq lignes de formules que de faire un dessin avec PSTricks…
Moi, personnellement, lorsque j’étais étudiant j’adorais les livres de Klaus Jänich, parus dans la série Undergraduate Texts in Mathematics chez Springer, très bien écrits et agrementés de nombreux dessins; en particulier son livre sur la topologie et son livre sur les fonctions holomorphes m’ont beaucoup aidé.
C’est cette démarche, avec beaucoup d’illustrations, que nous avons adoptée pour la rédaction de notre livre Mathématiques L1 pour la première année en université ou en classe prépa.

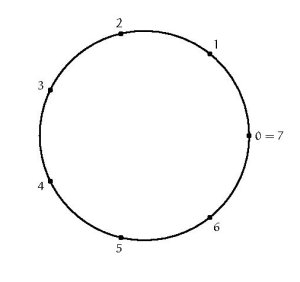
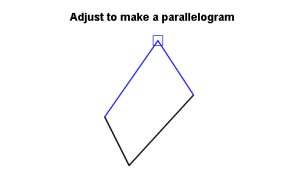
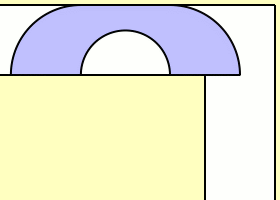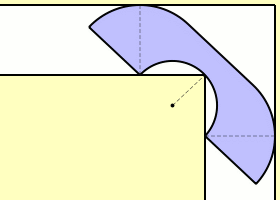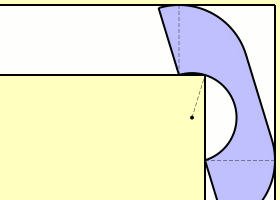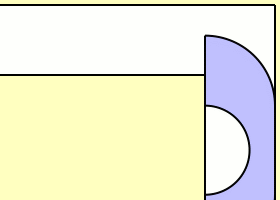

« la précision totale »:
Il faut quand même dire que une « pécision totale » n’existe pas même en mathématiques.
Plus généralement que la technique de Hand waving, dans la plupart des explications en mathématiques, on fait appel au sens commun qui reflète l’intuition derière la verité qu’on veut éclaircir, or les mathématiques contemporaine offre un certain nombre de structures dont l’imagination fut le premier ingredient pour les concevoir, cette imagination consiste, en vue de résolution d’un problème, à combiner de façon adéquate diverses structures, l’imagination est alors un moyen pour concevoir les vérités mathématiques qui sont généralement de caractère abstrait, l’abstraction ici continue ce qu’a déjà commencé l’intuition, les dessins en mathématiques peuvent donc être des pas audacieux pour poursuivre le chemin vers plus d’abstraction et plus de généralisation.