Une solution niveau CM2 pour les rectangles entiers

L’exercice amusant sur les rectangles entiers possède apparemment beaucoup de solutions. François-Xavier Vialard m’a indiqué un article en anglais de Stan Wagon qui réunit les différentes démonstrations de 14 auteurs du monde entier ! L’une parmi elles, qui m’a été signalé aussi par Tahar Boulmezaoud, est particulièrement belle. En effet, elle utilise seulement des mathématiques élémentaires que même un élève de 6^e, voire de CM2, peut comprendre. L’idée de la preuve est de travailler avec un réseau en forme d’échiquier. Voici une description détaillé de cette démonstration, lisible par tous, indépendemment du niveau en maths :

Je rappelle que l’énoncé de l’exercice se trouve ici.

On considère un grand échiquier dont chaque case est de longueur 1/2. Nous allons l’utiliser pour poser nos rectangles dessus.

Lemme 1. Si un rectangle est entier alors il couvre autant de surface noire que blanche.

Preuve : Cela se verra plus facilement avec un dessin. Voici un rectangle dont le coté horizontal est 3.

On le découpe,

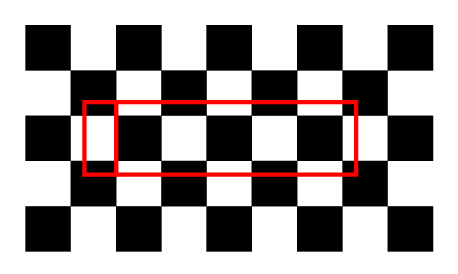
puis on déplace la partie gauche à droite, sans que cela ne change la superficie blanche ou noire couverte.

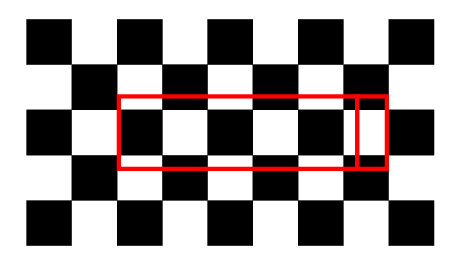
Il est maintenant évident que le rectangle couvre autant de superficie blanche que noire, ce qui achève la démonstration du lemme 1.

Remarque : La réciproque du lemme 1 n’est pas vraie. Comme contre-exemple il suffit de prendre un rectangle dont le milieu se trouve sur un point nœud de l’échiquier. Il couvre alors autant d’aire noire que blanche sans être pourtant nécessairement entier :

Mais si on rajoute une condition de plus les choses s’arrangent ! En effet, on a l’énoncé suivant.

Lemme 1. Si un rectangle dont au moins un sommet coïncide avec un point nœud de l’échiquier couvre autant de surface noire que blanche alors il est entier.

Preuve : Prenons le cas où le sommet en bas à gauche du rectangle coïncide avec un point nœud. Colorons ce nœud ainsi que les autres nœuds qui sont de coordonnées entières par rapport à lui. Nous supposons qu’aucun des autres trois sommets est sur un nœud coloré.

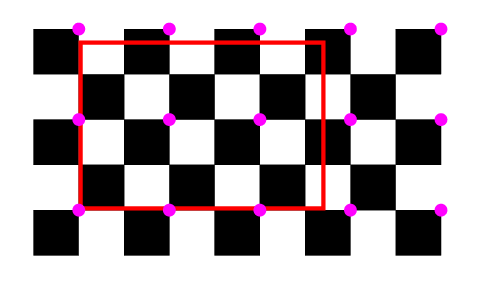
Pour examiner si le rectangle couvre autant de surface blanche que noire, nous le découpons ainsi :

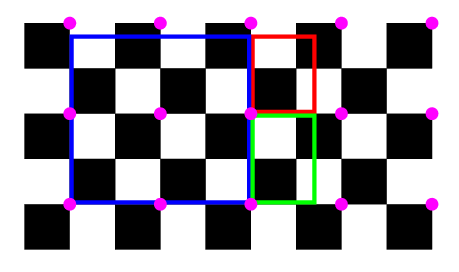
Le rectangle bleu a un côté horizontal entier et couvre donc, d’après le lemme 1, autant de surface noire que blanche. De même pour le rectangle vert car son côté vertical est entier.
Il reste alors à examiner le petit rectangle rouge.

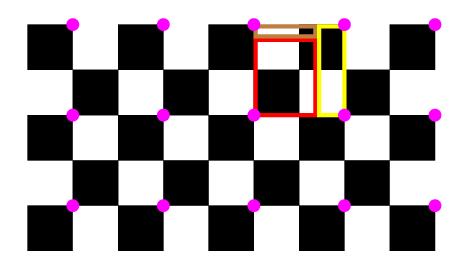
Le petit rectangle jaune couvre autant d’aire blanche que noire, tandis que le marron couvre plus d’aire blanche que noire. Par conséquence le petit rectangle rouge couvre plus de surface noire que blanche.

Nous avons donc démontré qu’un rectangle dont un unique sommet coïncide avec un nœud coloré
ne peut pas couvrir autant d’aire blanche que noire. Donc si un rectangle a au moins un sommet sur un nœud coloré et couvre la même aire blanche que noire alors il a forcément un deuxième sommet sur un nœud coloré, et cela implique qu’il s’agit d’un rectangle entier. Le lemme 2 est ainsi démontré.

Remarque : En réalité, il y a quatre types petits rectangles restants mais nous n’avons traité qu’un seul type car pour les trois autres on voit immédiatement que les aires blanches et noires ne sont pas les mêmes :

Maintenant nous sommes prêts à donner la preuve du problème posé.

Nous plaçons notre grand rectangle de manière qu’un de ses sommet est sur un point nœud de l’échiquier. Par hypothèse tous les petits rectangles le constituant sont entiers, donc chacun couvre, d’après le lemme 1, autant d’aire blanche et que noire. Il en est de même du grand rectangle. D’après le lemme 2 il est entier.